Quantum Physics-Informed Neural Networks
- PMID: 39202119
- PMCID: PMC11353915
- DOI: 10.3390/e26080649
Quantum Physics-Informed Neural Networks
Abstract
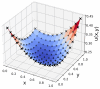
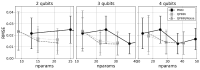
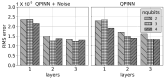
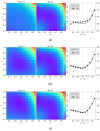
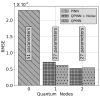
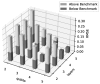
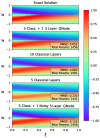
In this study, the PennyLane quantum device simulator was used to investigate quantum and hybrid, quantum/classical physics-informed neural networks (PINNs) for solutions to both transient and steady-state, 1D and 2D partial differential equations. The comparative expressibility of the purely quantum, hybrid and classical neural networks is discussed, and hybrid configurations are explored. The results show that (1) for some applications, quantum PINNs can obtain comparable accuracy with less neural network parameters than classical PINNs, and (2) adding quantum nodes in classical PINNs can increase model accuracy with less total network parameters for noiseless models.
Keywords: physics informed neural networks; quantum algorithms; quantum computing; quantum data-derived methods; quantum machine learning; quantum variational algorithm.
Conflict of interest statement
The authors declare no conflicts of interest.
Figures
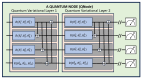
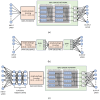

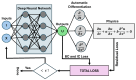

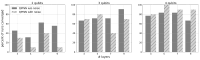

References
-
- Kieu T. Quantum Hypercomputation. [(accessed on 5 March 2024)];Minds Mach. 2002 12:541–561. doi: 10.1023/A:1021130831101. Available online: https://api.semanticscholar.org/CorpusID:10368720. - DOI
-
- D-Wave Ocean Software Documentation. [(accessed on 1 January 2024)]. Available online: https://www.dwavesys.com/solutions-and-products/ocean.
-
- Aleksandrowicz G., Alexander T., Barkoutsos P., Bello L., Ben-Haim Y., Bucher D., Cabrera-Hernández F.J., Carballo-Franquis J., Chen A., Chen C. Qiskit: An Open-Source Framework for Quantum Computing. Jan, 2019. [(accessed on 13 August 2021)]. Available online: https://zenodo.org/records/2562111.
-
- IBM Learning Quantum Computation Using Qiskit. [(accessed on 1 June 2021)]. Available online: http://qiskit.org/textbook.
-
- Steiger D., Häner T., Troyer M. ProjectQ: An open source software framework for quantum computing. Quantum. 2018;2:49. doi: 10.22331/q-2018-01-31-49. - DOI
Grants and funding
LinkOut - more resources
Full Text Sources

