Poisson Kalman filter for disease surveillance
- PMID: 39211287
- PMCID: PMC11360429
- DOI: 10.1103/physrevresearch.2.043028
Poisson Kalman filter for disease surveillance
Abstract
An optimal filter for Poisson observations is developed as a variant of the traditional Kalman filter. Poisson distributions are characteristic of infectious diseases, which model the number of patients recorded as presenting each day to a health care system. We develop both a linear and a nonlinear (extended) filter. The methods are applied to a case study of neonatal sepsis and postinfectious hydrocephalus in Africa, using parameters estimated from publicly available data. Our approach is applicable to a broad range of disease dynamics, including both noncommunicable and the inherent nonlinearities of communicable infectious diseases and epidemics such as from COVID-19.
Figures



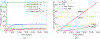
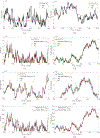

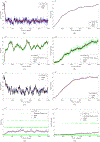
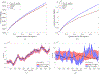
References
-
- Zaman G, Kang YH, and Jung IH, Proc. KSIAM 3, 31 (2007).
-
- Yusuf TT and Benyah F, World J. Model. Simul 8, 194 (2012).
-
- Zaman G, Kang YH, and Jung IH, BioSystems 93, 240 (2008). - PubMed
-
- Sharomi O and Malik T, Ann. Oper. Res 251, 55 (2017).
-
- Di Giamberardino P and Iacoviello D, Proceedings of the 2019 23rd International Conference on System Theory, Control and Computing (ICSTCC) (IEEE, Piscataway, 2019), pp. 733–738.
Grants and funding
LinkOut - more resources
Full Text Sources
