Entanglement-induced collective many-body interference

Abstract

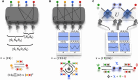
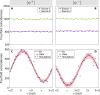
Entanglement and interference are both hallmark effects of quantum physics. Particularly rich dynamics arise when multiple (at least partially) indistinguishable particles are subjected to either of these phenomena. By combining both entanglement and many-particle interference, we propose an interferometric setting through which N-particle interference can be observed, while any interference of lower orders is strictly suppressed. We experimentally demonstrate this effect in a four-photon interferometer, where the interference is nonlocal, in principle, as only pairs of photons interfere at two separate and independent beam splitters. A joint detection of all four photons identifies a high-visibility interference pattern varying as a function of their collective four-particle phase, a genuine four-body property.

Fig. 1.. Many-particle interference and collective phases.

(A) In a fully connected interferometer with single-particle unitary matrix U (here 4 × 4), multiple exchange processes among combinations of input-output channels contribute to specific output events. The reduced 2P state associated with the second (yellow) and the fourth (red) particles contributes to the two-point correlator 〈N₃N₄〉 via the 2P transitions indicated by the solid and dashed lines. The interference of these two 2P paths is encoded in the 2P coherence at the bottom of the panel, which is associated with the permutation π = (1 2) obtained by taking one 2P path in the forward direction (dashed lines) followed by the other one in the backward direction (solid lines) (60). The matrix elements of U weigh these contributions, as well as the contributions from all other 2P sets. Similar considerations apply to all correlators from combinations of different output modes. (B) The four-particle (4P) coherence corresponding to the depicted four-cyclic permutation leads to a genuine 4P interference that depends on a collective phase ϕ. This collective phase is set by the summation of phases ϕ_ij (see section on Many-body interference and collective phases), resulting from the overlaps of the particles’ internal states along a “circle-dance” graph representative of the permutation process (35, 36), as depicted at the bottom of the panel. (C) A genuine entanglement-induced 4P interference can be achieved by interfering entangled particles (blue envelope) with particles in separable states in two independent and separate beam splitters. In this process, the entanglement induces a collective 4P phase term ϕ, set by the internal states of all particles, through the two 2P permutations in π = (1 2)(3 4). The collective phase ϕ only affects the four-point correlator and introduces full-contrast interference fringes: 〈N₁N₂N₃N₄〉 ∝ cos²(ϕ/2) (see section on Scheme for entanglement-induced collective interference).

Fig. 2.. Experimental setup.

(A) A picosecond (ps)–pulsed laser clocked at 80 MHz is split via a balanced beam splitter (BS) to pump two SPDC sources based on apodized potassium titanyl phosphate (aKTP) crystals embedded in Sagnac interferometers (source 1 and source 2). Half-wave plates (HWPs) and Glan-Taylor polarizers (GT) are used to adjust the input power and set the pump polarization to obtain entangled photon pairs (source 1) or separable photon pairs (source 2). Down-converted photons are separated from the laser light via polarizing beam splitters (PBSs), dichroic mirrors (DMs), long-pass filters (LPFs), and collected through single-mode fibers. (B) Photons are adjusted in polarization via combinations of HWPs and quarter-wave plates (QWPs), or via fiber polarization controllers (FPCs) and guided to two independent balanced beam splitters. At the output, photons are detected by multiplexing each output channel (Ch. A to Ch. D) with two SNSPDs at the output ports of a PBS, as shown in the inset. The single-photon detection events are analyzed at a field-programmable gate array (FPGA) logic unit and post-processed to determine every twofold, threefold, and fourfold coincidence event.

Fig. 3.. Results of fourfold coincidence counts for entanglement-induced collective 4P interference.

(A and B) Fourfold background coincidences from multi-pair emissions of individual sources. (C and D) Background-subtracted fourfold coincidences data (blue dots) fitted with a cosine function (red curve). The red-shaded region shows the fit prediction interval at a confidence level of one SD. The graphs include the results of the multiphoton interference simulations (black dashed curve). The visibility of the fit is 69.2(2.5)% and 85.8(4.5)% for (C) and (D), respectively. Simulations (Supplementary Note 5) predict a visibility of 70.2(1.2)% and 88.1(1.7)%. The integration time for each point of all panels is 60 s.