Non-local interaction in discrete Ricci curvature-induced biological aggregation

Abstract

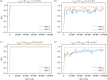
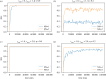
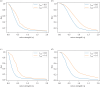
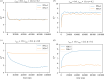
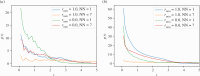
We investigate the collective dynamics of multi-agent systems in two- and three-dimensional environments generated by minimizing discrete Ricci curvature with local and non-local interaction neighbourhoods. We find that even a single effective topological neighbour suffices for significant order in a system with non-local topological interactions. We also explore topological information flow patterns and clustering dynamics using Hodge spectral entropy and mean Forman-Ricci curvature.

Keywords: applied mathematics; biocomplexity; biophysics.

Figure 1.

0-simplex is a vertex, 1-simplex is an edge, 2-simplex is a filled triangle and 3-simplex is a filled tetrahedron.

Figure 2.

Schematic representation of the simplicial complex (up to edges) structure and the neighbouring agents in an annular region around an agent.

Figure 3.

Time evolution of order parameter for the two-dimensional case. $\mathrm{NN}$ denotes the number of effective neighbours being considered. It is to be noted that when $⟨{\varphi }_v⟩\approx 1.0$, the lines for $\mathrm{NN}=1$ get buried below that for $\mathrm{NN}=7$. (a) for $r_{min}=0.0$ and noise strength $\eta =0.0$, (b) for $r_{min}=0.0$ and noise strength $\eta =0.2$, (c) for $r_{min}=1.0$ and noise strength $\eta =0.0$ and (d) for $r_{min}=1.0$ and noise strength $\eta =0.2$.

Figure 4.

Time evolution of order parameter for the three-dimensional case. $\mathrm{NN}$ denotes the number of effective neighbours being considered. It is to be noted that when $⟨{\varphi }_v⟩\approx 1.0$, the lines for $\mathrm{NN}=1$ get buried below that for $\mathrm{NN}=7$. (a) for $r_{min}=0.0$ and noise strength $\eta =0.0$, (b) for $r_{min}=0.0$ and noise strength $\eta =0.2$, (c) for $r_{min}=1.0$ and noise strength $\eta =0.0$ and (d) for $r_{min}=1.0$ and noise strength $\eta =0.2$.

Figure 5.

The variation of the mean of the Ricci curvature $R$ as the noise strength ($\eta$) varies. (a) $\mathrm{NN}=1$ in two dimensions, (b) $\mathrm{NN}=7$ in two dimensions, (c) $\mathrm{NN}=1$ in three dimensions and (d) $\mathrm{NN}=7$ in three dimensions.

Figure 6.

The variation of the mean order parameter $⟨{\varphi }_v⟩$ as the noise strength ($\eta$) varies. (a) $\mathrm{NN}=1$ in two dimensions, (b) $\mathrm{NN}=7$ in two dimensions, (c) $\mathrm{NN}=1$ in three dimensions and (d) $\mathrm{NN}=7$ in three dimensions.

Figure 7.

Time evolution of Hodge Spectral entropy $S_k^{hs}$ for the local and non-local model in two-dimensional periodic box. (a) $S_0^{hs}$ with $r_{min}=0$, (b) $S_1^{hs}$ with $r_{min}=0$, (c) $S_0^{hs}$ with $r_{min}=1.0$ and (d) $S_1^{hs}$ with $r_{min}=1.0$.

Figure 8.

Time evolution of Hodge Spectral entropy $S_k^{hs}$ for the local and non-local model in three-dimensional periodic box. (a) $S_0^{hs}$ with $r_{min}=0$, (b) $S_1^{hs}$ with $r_{min}=0$, (c) $S_0^{hs}$ with $r_{min}=1.0$ and (d) $S_1^{hs}$ with $r_{min}=1.0$.

Figure 9.

Radial distribution function $g(r)$ with $\eta =0.2$. (a) in two dimensions and (b) in three dimensions.