Emergence of metastability in frustrated oscillatory networks: the key role of hierarchical modularity
- PMID: 39233777
- PMCID: PMC11372895
- DOI: 10.3389/fnetp.2024.1436046
Emergence of metastability in frustrated oscillatory networks: the key role of hierarchical modularity
Abstract
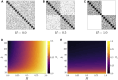
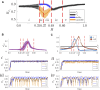
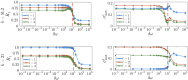
Oscillatory complex networks in the metastable regime have been used to study the emergence of integrated and segregated activity in the brain, which are hypothesised to be fundamental for cognition. Yet, the parameters and the underlying mechanisms necessary to achieve the metastable regime are hard to identify, often relying on maximising the correlation with empirical functional connectivity dynamics. Here, we propose and show that the brain's hierarchically modular mesoscale structure alone can give rise to robust metastable dynamics and (metastable) chimera states in the presence of phase frustration. We construct unweighted 3-layer hierarchical networks of identical Kuramoto-Sakaguchi oscillators, parameterized by the average degree of the network and a structural parameter determining the ratio of connections between and within blocks in the upper two layers. Together, these parameters affect the characteristic timescales of the system. Away from the critical synchronization point, we detect the emergence of metastable states in the lowest hierarchical layer coexisting with chimera and metastable states in the upper layers. Using the Laplacian renormalization group flow approach, we uncover two distinct pathways towards achieving the metastable regimes detected in these distinct layers. In the upper layers, we show how the symmetry-breaking states depend on the slow eigenmodes of the system. In the lowest layer instead, metastable dynamics can be achieved as the separation of timescales between layers reaches a critical threshold. Our results show an explicit relationship between metastability, chimera states, and the eigenmodes of the system, bridging the gap between harmonic based studies of empirical data and oscillatory models.
Keywords: chimera states; criticality; hierarchical modularity; metastability; network physiology; oscillations; renormalisation; whole-brain.
Copyright © 2024 Caprioglio and Berthouze.
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures
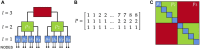





Similar articles
-
Emergence of metastable dynamics in functional brain organization via spontaneous fMRI signal and whole-brain computational modeling.Annu Int Conf IEEE Eng Med Biol Soc. 2017 Jul;2017:4471-4474. doi: 10.1109/EMBC.2017.8037849. Annu Int Conf IEEE Eng Med Biol Soc. 2017. PMID: 29060890
-
Metastability and chimera states in modular delay and pulse-coupled oscillator networks.Chaos. 2012 Dec;22(4):043131. doi: 10.1063/1.4766592. Chaos. 2012. PMID: 23278066
-
Emergence of multiple spontaneous coherent subnetworks from a single configuration of human connectome coupled oscillators model.Sci Rep. 2024 Dec 28;14(1):30726. doi: 10.1038/s41598-024-80510-2. Sci Rep. 2024. PMID: 39730441 Free PMC article.
-
Dynamic Computation in Visual Thalamocortical Networks.Entropy (Basel). 2019 May 16;21(5):500. doi: 10.3390/e21050500. Entropy (Basel). 2019. PMID: 33267214 Free PMC article. Review.
-
Emergence of Hierarchical Modularity in Evolving Networks Uncovered by Phylogenomic Analysis.Evol Bioinform Online. 2019 Sep 5;15:1176934319872980. doi: 10.1177/1176934319872980. eCollection 2019. Evol Bioinform Online. 2019. PMID: 31523127 Free PMC article. Review.
Cited by
-
Metastable Oscillatory Modes as a Signature of Entropy Management in the Brain.Entropy (Basel). 2024 Dec 3;26(12):1048. doi: 10.3390/e26121048. Entropy (Basel). 2024. PMID: 39766677 Free PMC article.
References
-
- Alteriis G. de, MacNicol E., Hancock F., Ciaramella A., Cash D., Expert P., et al. (2024). EiDA: a lossless approach for dynamic functional connectivity; application to fMRI data of a model of ageing. Imaging Neurosci. 2, 1–22. 10.1162/imag_a_00113 - DOI
-
- Arenas A., Díaz-Guilera A. (2007). Synchronization and modularity in complex networks. Eur. Phys. J. Special Top. 143 (1), 19–25. 10.1140/epjst/e2007-00066-2 - DOI
-
- Arenas A., Díaz-Guilera A., Kurths J., Moreno Y., Zhou C. (2008). Synchronization in complex networks. Phys. Rep. 469 (3), 93–153. 10.1016/j.physrep.2008.09.002 - DOI
LinkOut - more resources
Full Text Sources
Miscellaneous

