Emergence of metastability in frustrated oscillatory networks: the key role of hierarchical modularity
- PMID: 39233777
- PMCID: PMC11372895
- DOI: 10.3389/fnetp.2024.1436046
Emergence of metastability in frustrated oscillatory networks: the key role of hierarchical modularity
Abstract
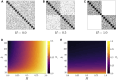
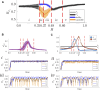
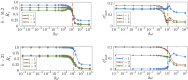
Oscillatory complex networks in the metastable regime have been used to study the emergence of integrated and segregated activity in the brain, which are hypothesised to be fundamental for cognition. Yet, the parameters and the underlying mechanisms necessary to achieve the metastable regime are hard to identify, often relying on maximising the correlation with empirical functional connectivity dynamics. Here, we propose and show that the brain's hierarchically modular mesoscale structure alone can give rise to robust metastable dynamics and (metastable) chimera states in the presence of phase frustration. We construct unweighted 3-layer hierarchical networks of identical Kuramoto-Sakaguchi oscillators, parameterized by the average degree of the network and a structural parameter determining the ratio of connections between and within blocks in the upper two layers. Together, these parameters affect the characteristic timescales of the system. Away from the critical synchronization point, we detect the emergence of metastable states in the lowest hierarchical layer coexisting with chimera and metastable states in the upper layers. Using the Laplacian renormalization group flow approach, we uncover two distinct pathways towards achieving the metastable regimes detected in these distinct layers. In the upper layers, we show how the symmetry-breaking states depend on the slow eigenmodes of the system. In the lowest layer instead, metastable dynamics can be achieved as the separation of timescales between layers reaches a critical threshold. Our results show an explicit relationship between metastability, chimera states, and the eigenmodes of the system, bridging the gap between harmonic based studies of empirical data and oscillatory models.
Keywords: chimera states; criticality; hierarchical modularity; metastability; network physiology; oscillations; renormalisation; whole-brain.
Copyright © 2024 Caprioglio and Berthouze.
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures
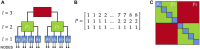





References
-
- Alteriis G. de, MacNicol E., Hancock F., Ciaramella A., Cash D., Expert P., et al. (2024). EiDA: a lossless approach for dynamic functional connectivity; application to fMRI data of a model of ageing. Imaging Neurosci. 2, 1–22. 10.1162/imag_a_00113 - DOI
-
- Arenas A., Díaz-Guilera A. (2007). Synchronization and modularity in complex networks. Eur. Phys. J. Special Top. 143 (1), 19–25. 10.1140/epjst/e2007-00066-2 - DOI
-
- Arenas A., Díaz-Guilera A., Kurths J., Moreno Y., Zhou C. (2008). Synchronization in complex networks. Phys. Rep. 469 (3), 93–153. 10.1016/j.physrep.2008.09.002 - DOI
LinkOut - more resources
Full Text Sources
Miscellaneous

