Cavity Floquet engineering
- PMID: 39237571
- PMCID: PMC11377740
- DOI: 10.1038/s41467-024-52014-0
Cavity Floquet engineering
Abstract
Floquet engineering is a promising tool to manipulate quantum systems coherently. A well-known example is the optical Stark effect, which has been used for optical trapping of atoms and breaking time-reversal symmetry in solids. However, as a coherent nonlinear optical effect, Floquet engineering typically requires high field intensities obtained in ultrafast pulses, severely limiting its use. Here, we demonstrate using cavity engineering of the vacuum modes to achieve orders-of-magnitude enhancement of the effective Floquet field, enabling Floquet effects at an extremely low fluence of 450 photons/μm2. At higher fluences, the cavity-enhanced Floquet effects lead to 50 meV spin and valley splitting of WSe2 excitons, corresponding to an enormous time-reversal breaking, non-Maxwellian magnetic field of over 200 T. Utilizing such an optically controlled effective magnetic field, we demonstrate an ultrafast, picojoule chirality XOR gate. These results suggest that cavity-enhanced Floquet engineering may enable the creation of steady-state or quasi-equilibrium Floquet bands, strongly non-perturbative modifications of materials beyond the reach of other means, and application of Floquet engineering to a wide range of materials and applications.
© 2024. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures

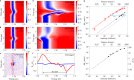

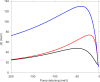
References
-
- Autler, S. H. & Townes, C. H. Stark effect in rapidly varying fields. Phys. Rev.100, 703 (1955). 10.1103/PhysRev.100.703 - DOI
-
- Jaynes, E. & Cummings, F. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE51, 89 (1963). 10.1109/PROC.1963.1664 - DOI
-
- Shirley, J. H. Solution of the Schrödinger equation with a Hamiltonian periodic in time. Phys. Rev.138, B979 (1965). 10.1103/PhysRev.138.B979 - DOI
Grants and funding
- W911NF-17-1-0312/United States Department of Defense | United States Army | U.S. Army Research, Development and Engineering Command | Army Research Office (ARO)
- FA2386-21-1-406/United States Department of Defense | United States Air Force | AFMC | Air Force Office of Scientific Research (AF Office of Scientific Research)
- DMR 213247/National Science Foundation (NSF)
- N00014-21-1-277/United States Department of Defense | United States Navy | Office of Naval Research (ONR)
- GBMF10694/Gordon and Betty Moore Foundation (Gordon E. and Betty I. Moore Foundation)
LinkOut - more resources
Full Text Sources

