Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2024 Aug 9;10(16):e35818.
doi: 10.1016/j.heliyon.2024.e35818. eCollection 2024 Aug 30.

A conformable mathematical model of Ebola Virus Disease and its stability analysis

Nadeem Abbas  1 , Syeda Alishwa Zanib  2 , Sehrish Ramzan  3 , Aqsa Nazir  4 , Wasfi Shatanawi  1   5   6
Affiliations

A conformable mathematical model of Ebola Virus Disease and its stability analysis

Nadeem Abbas et al. Heliyon. .

Abstract

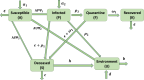
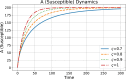
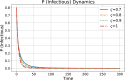
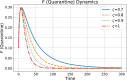
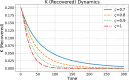
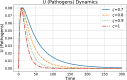
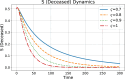
Ebola Virus Disease (EVD) is a viral hemorrhagic fever that affects humans and other primates. It is characterized by rapid virus spread in a short period of time. The disease has the potential to spread to many different regions of the world. In this paper, we have developed a modified mathematical model of the Ebola virus, adding the quarantine population as a control strategy. The quarantine population F and parameters ρ 3 represent the rate at which individuals enter the quarantine compartment, which is vital in controlling the virus spread within society. The conformable derivatives have been applied to the modified model to observe the behavior of individuals for fractional derivative values between 0.7 and 1. For a modified model, the threshold parameter ( R 0 ) has been determined using the Next-Generation Matrix (NGM) method. We have checked local and global stability at a disease-free equilibrium point using Routh-Herwitz (RH) criteria and Castillo-Chavez, respectively. Numerical results obtained through the Fourth-Order Runge Kutta Method (RK4) demonstrate, a decrease in the virus transmission rate after following the implementation of the quarantine strategy.

Keywords: Disease-free equilibrium point; Epidemic disease; Global stability; Local stability; Next-generation matrix.

PubMed Disclaimer

Conflict of interest statement

All the authors have no declaration of interest in the manuscript.

Figures

Figure 1
Figure 1
Flowchart of EVD Model.
Figure 2
Figure 2
Susceptible Dynamics A(ζ).
Figure 3
Figure 3
Infectious Dynamics P(ζ).
Figure 4
Figure 4
Quarantine Dynamics F(ζ).
Figure 5
Figure 5
Recovered Dynamics K(ζ).
Figure 6
Figure 6
Ebola Virus Pathogens in the Environment U(ζ).
Figure 7
Figure 7
Deceased Dynamics S(ζ).
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Jacob S.T., Crozier I., Fischer W.A., Hewlett A., Kraft C.S., Vega M.A.D.L., Soka M.J., Wahl V., Griffiths A., Bollinger L., Kuhn J.H. Ebola virus disease. Nat. Rev. Dis. Primers. 2020;6(1):13. doi: 10.1038/s41572-020-0147-3. - DOI - PMC - PubMed
    1. Ahmad M.D., Usman M., Khan A., Imran M. Optimal control analysis of Ebola disease with control strategies of quarantine and vaccination. Infect. Dis. Poverty. 2016;5:1–12. doi: 10.1186/s40249-016-0161-6. - DOI - PMC - PubMed
    1. Zanib S.A., Ramzan S., Abbas N., et al. A mathematical approach to drug addiction and rehabilitation control dynamic. Model. Earth Syst. Environ. 2024:1–8. doi: 10.1007/s40808-023-01931-y. - DOI
    1. Singh J.P., Abdeljawad T., Baleanu D., Kumar S. Transmission dynamics of a novel fractional model for the Marburg virus and recommended actions. Eur. Phys. J. Spec. Top. 2023;232(14):2645–2655. doi: 10.1140/epjs/s11734-023-00943-0. - DOI
    1. Naik P.A. Global dynamics of a fractional-order SIR epidemic model with memory. Int. J. Biomath. 2020;13(08):2050071. doi: 10.1142/s1793524520500710. - DOI

LinkOut - more resources