The zero-and-plus/minus-one inflated extended-Poisson distribution
- PMID: 39247656
- PMCID: PMC11378118
- DOI: 10.1080/02664763.2023.2260570
The zero-and-plus/minus-one inflated extended-Poisson distribution
Abstract
In this paper, we introduce a new distribution defined on , called the distribution, which can be viewed as a natural extension of the zero-and-one-inflated Poisson ( ) distribution. It is designed to fit the count data with potentially excess zeros and/or ones, and/or minus ones. We explore its various properties and investigate the estimation of the unknown parameters. Moreover, simulation experiments are carried out to attest to the performance of the estimation. Through the use of a useful data set on football scores, the applicability of the proposed distribution is examined.
Keywords:
Zero-and-one-inflated Poisson distribution; count data analysis; discrete distribution defined on
© 2023 Informa UK Limited, trading as Taylor & Francis Group.
Conflict of interest statement
No potential conflict of interest was reported by the author(s).
Figures
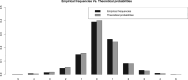
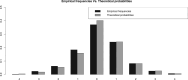
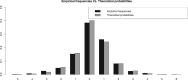
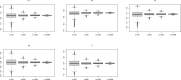



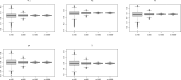

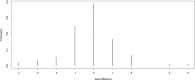
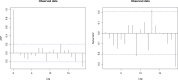
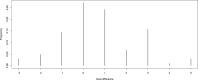
References
-
- Alzaid A.A. and Omair M.A., On the Poisson difference distribution inference and applications, Bull. Malays. Math. Sci. Soc. Second Ser. 33 (2010), pp. 17–45.
-
- Bakouch H.S., Kachour M., and Nadarajah S., An extended Poisson distribution, Commun. Stat. Theory Methods 45 (2016), pp. 6746–6764.
-
- Bulla J., Chesneau C., and Kachour M., On the bivariate Skellam distribution, Commun. Stat. Theory Methods 44 (2015), pp. 4552–4567.
-
- Cameron A.C. and Trivedi P.K., Regression Analysis of Count Data, Vol. 53, Cambridge University Press, 2013.
LinkOut - more resources
Full Text Sources
