Quantitative metrics commonly derived from diffusion tractography covary with streamline length: a characterization and method of adjustment

Abstract

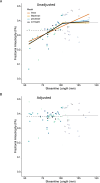
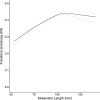
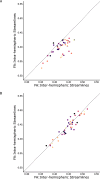
Tractography algorithms are used extensively to delineate white matter structures, by operating on the voxel-wise information generated through the application of diffusion tensor imaging (DTI) or other models to diffusion weighted (DW) magnetic resonance imaging (MRI) data. Through statistical modelling, we demonstrate that these methods commonly yield substantial and systematic associations between streamline length and several tractography derived quantitative metrics, such as fractional anisotropy (FA). These associations may be described as piecewise linear. For streamlines shorter than an inflection point (determined for a group of tracts delineated for each individual brain), estimates of FA exhibit a positive linear relation with streamline length. For streamlines longer than the point of inflection, the association is weaker, with the slope of the relationship between streamline length and FA differing only marginally from zero. As the association is most pronounced for a range of streamline lengths encountered typically in DW imaging of the human brain (less than ~ 100 mm), our results suggest that some quantitative metrics derived from diffusion tractography have the potential to mislead, if variations in streamline length are not considered. A method is described, whereby an Akaike information weighted average of linear, Blackman and piecewise linear model predictions, may be used to compensate effectively for the association of FA (and other quantitative metrics) with streamline length, across the entire range of streamline lengths present in each specimen.

Keywords: Brain mapping; Data interpretation; Human; Neural pathways; Neuroanatomical tract-tracing techniques; White matter.

Fig. 1

For illustrative purposes, the theoretical estimate of a quantitative metric, such as FA, along a streamline is modelled as increasing with streamline length from a termination magnitude threshold of 0.2, at a rate equivalent to an increase of 1.6 for every change of 100 units of length. It is further assumed that the quantitative metric is constrained to a range of 0 to 1. Given these parameters, the terminal sections (less than 50 units of length) – at both ends of the streamline, are characterised by all values being lower than 1. It is specified that in these regions the slope is constant, and independent of the overall length of the streamline. Within centre (non-terminal) sections, all values are equal to 1 (the theoretical asymptote). Average estimates of the quantitative metric of (i.e., for an entire streamline) will therefore increase in a linear fashion with increases in streamline length (Panels A to J), up to the length at which the upper limit of 1 is reached (i.e., encompassing only the two terminal sections). For streamlines in excess of this length (i.e., also encompassing a centre section) (Panels K to T), the estimate of the quantitative metric will then increase as a power function with further increments in greater streamline length (Panel U). Crucially however, the tissue of real specimens will be characterised by estimates of the quantitative metric (e.g., FA) that are lower than the theoretical average. That is, the values obtained empirically will not continue to increase towards the theoretical limit (1) with increases in streamline length. In the present illustration, a maximum value of 0.7 is assumed. It follows that for this specimen the empirical average will remain 0.7 for all streamline lengths for which the theoretical model predicts a value of 0.7 or above. It would be anticipated therefore that the average estimate of the quantitative metric will increase in a linear fashion until the streamline length at which a value of 0.7 is obtained and remain constant (slope equal to zero) for streamlines in excess of this length (Panel V). For Panels A to T, the length (l) of the streamline and the proportion (p̂) of the streamline comprised of terminal sections (less than 50 units of length) are indicated

Fig. 2

Theoretical fits to the Blackman (also known as a linear-plateau) function are illustrated. In this example, notional data from three specimens are shown to differ only with respect to the asymptotic value of the derived estimate of a quantitative metric (e.g., FA). Specimen 1 (orange *) exhibits an asymptotic value of 0.72; Specimen 2 (blue ×) exhibits an asymptotic value of 0.80; and Specimen 3 (green +) exhibits an asymptotic value of 0.88. The streamline length corresponding to the start of the plateau region (the point of inflection) varies accordingly. In these examples, the slope of the initial segment is equivalent in each case. Empirical fits derived using the Blackman function can however also vary with respect to the slope of the initial segment. Furthermore, variations in the asymptotic value can covary with the streamline length at which the start of the plateau region occurs (Archontoulis and Miguez 2015)

Fig. 3

A Empirical fits to each of the three candidate models (linear (red), Blackman (orange), and piecewise-linear (blue), and the model averaged fit (black), are shown for the 84 tracts delineated for a single individual. The Akaike weights for the respective models were as follows: linear – 0.007; Blackman – 0.564; piecewise-linear – 0.270. The point of inflection was determined to be 103.0 mm for the Blackman model (FA = 0.390), 102.0 mm for the piecewise-linear model (FA = 0.383), and 102.7 mm for the averaged model (FA = 0.388). The slope of the initial segment was estimated to be 0.003 for the Blackman model, the piecewise-linear model, and the averaged model. The slope of the second segment was estimated to be 0.0002 for the averaged model. B The FA values, adjusted for the influence of streamline length (through the application of a model averaging approach), are plotted for the same individual. In both panels, the colours are assigned to tracts in the order in which they are listed in the source data. Values corresponding to streamline lengths shorter than the inflection point are assigned closed symbols, and values corresponding to streamline lengths longer than the inflection point are assigned open symbols. In both panels, the horizontal dotted line corresponds to the median FA value of tracts with streamline lengths longer than the inflection point. In each case, the horizontal dashed line corresponds to the median FA value of tracts with streamline lengths shorter than the inflection point

Fig. 4

A summary representation of the results obtained through the application of a model averaging approach to the predicted FA values generated by the three candidate models (linear, Blackman, and piecewise-linear), for the 43 participants included in Ruddy et al. (2017). For each participant, the models were evaluated, and the predictions weighted and averaged, at a range of nominal streamline lengths (at 1 mm intervals). This range spanned the median minimum streamline length and the median maximum streamline length observed across the 43 participants. The solid line corresponds to the means of the weighted, averaged, predicted values derived from 1000 bootstrapped samples. The dashed line was generated using the lower 95% confidence interval of the bootstrapped samples. The dotted line was generated using the upper 95% confidence interval. It is apparent that, for streamlines shorter than approximately 100 mm, there is an association between FA and streamline length

Fig. 5

Separately for each of the 43 participants included in Ruddy et al. (2017), and for each tract, the difference between the original FA value, and the FA value adjusted for the influence of streamline length (through the application of a model averaging approach) was calculated. The filled symbols correspond to the means of these difference values, when derived from 1000 bootstrapped samples drawn from the set of 43 participants (i.e., calculated separately for each tract). For a tract to be included, it was necessary that at least half of the participants must have contributed data (i.e., streamlines were resolved). The error bars correspond to the 95% confidence intervals of the bootstrapped samples. The tracts are plotted in order of mean streamline length (calculated across participants)

Fig. 6

The left portion of the figure (“Unadjusted FA values”) displays the rank ordering of unadjusted FA values obtained for streamlines (n = 26 tracts) that originate and terminate within the right cerebral hemisphere. The right portion of the figure (“Adjusted FA values”) displays the rank ordering of FA values that have been adjusted for streamline length in the manner described in the text. The size of each symbol (in the legend shown in the range 0.30–0.55) corresponds to the associated FA value (i.e., derived for that tract). The position of each symbol in relation to the y axis scale corresponds to the ranking of the FA value with respect to the set of 26 tracts. Those with a higher ranking (larger FA value) appear above those with a lower ranking (smaller FA value). While the assignation of fill colour to the individual tracts is arbitrary, as it remains consistent across panels A and B, it aids in the identification of differences in ranking (i.e., unadjusted versus adjusted). In both panels, the colours (which do not relate to FA value) are assigned to tracts in the order in which they are listed in the source data. The x axis is categorical. Tracts are plotted with respect to the x axis in the order in which they are listed in the source data. It is apparent that the rank ordering of the adjusted values (Panel B) is dramatically different from that of the unadjusted values (Panel A). M1a anterior primary motor cortex, M1p posterior and primary motor cortex, PMd dorsal premotor cortex, PMv and ventral premotor cortex, SMA proper—supplementary motor area proper, pre-SMA pre-supplementary motor area, S1- primary sensory cortex, CMA cingulate motor area. Three exemplars are highlighted via arrows between the unadjusted and adjusted values. The adjusted ranking (and FA value) for the S1-SMA tract is markedly higher than the unadjusted ranking (and value). The adjusted ranking for the CMA-M1a tract is lower than the unadjusted ranking. In respect of the PMd-preSMA tract, the ranking of the adjusted and unadjusted FA values is the same

Fig. 7

The trimmed mean (trimming = 20%) of the FA values derived for all inter-hemispheric tracts for which streamlines were resolved for each participant, and the trimmed mean of the FA values derived for all right hemisphere intra-hemispheric tracts for which streamlines were resolved for each participant, were calculated. Unadjusted FA values are shown in Panel A. FA values that have been adjusted for streamline length in the manner described in the text are shown in Panel B. Each point represents the data for a single participant, with the colour coding determined by the order in which the 43 participants are listed in the source data. In both panels, the x coordinate for each point corresponds to the trimmed mean FA value for the right hemisphere tracts, and the y coordinate corresponds to the trimmed mean FA value for the inter-hemispheric tracts. Points lying close to the line of equality indicate similarity in the FA values obtained for inter-hemispheric and right hemisphere streamlines. Points lying below the line of equality indicate FA values for the right hemisphere streamlines that are lower than those for the inter-hemispheric streamlines. Comparison of the plots generated for the unadjusted data (Panel A) and the adjusted data (Panel B) makes apparent that differences between right hemisphere and inter-hemispheric FA values present for the unadjusted data, are not apparent for the adjusted data. The results of corresponding inferential tests are reported in the text

Fig. 8

Empirical fits to each of the three candidate models (linear (red), Blackman (orange), and piecewise-linear (blue), and the model averaged fit (black), are shown for three example tracts. Each point represents the data for a single participant, with the colour coding determined by the order in which the 43 participants are listed in the source data. A. Between left cingulate motor area (CMA) and left dorsal premotor cortex (PMd). B Between left CMA and right anterior primary motor cortex (M1a). C Between left PMd and right PMd