Three-dimensional valley-contrasting sound

Abstract

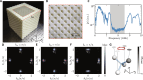
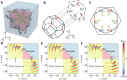
Spin and valley are two fundamental properties of electrons in crystals. The similarity between them is well understood in valley-contrasting physics established decades ago in two-dimensional (2D) materials like graphene-with broken inversion symmetry, the two valleys in graphene exhibit opposite orbital magnetic moments, similar to the spin-1/2 behaviors of electrons, and opposite Berry curvature that leads to a half topological charge. However, valley-contrasting physics has never been explored in 3D crystals. Here, we develop a 3D acoustic crystal exhibiting 3D valley-contrasting physics. Unlike spin that is fundamentally binary, valley in 3D can take six different values, each carrying a vortex in a distinct direction. The topological valley transport is generalized from the edge states of 2D materials to the surface states of 3D materials, with interesting features including robust propagation, topological refraction, and valley-cavity localization. Our results open a new route for wave manipulation in 3D space.

Fig. 1.. Vectorial valley-contrasting physics in a 3D acoustic crystal.

(A and B) Cubic cell (A) and unit cell (B) of the valley acoustic crystal, with the lattice vectors a₁ = (a/2, a/2,0), a₂ = (0, a/2, a/2), and a₃ = (a/2,0, a/2). The gray region is filled with air, and the yellow shells represent rigid walls. (C) First BZ, with the six valleys denoted by colored markers. Gray dashes indicate the nodal lines for Δ = 0. (D) Bulk dispersion of the acoustic crystal. Gray and blue curves correspond to the cases where Δ = 0 and Δ = 1 mm, respectively. (E to J) Bloch modes for the lowest band at the six valleys. The blue and gray colors denote the amplitude and phase of the pressure field, and the red arrows indicate the power flow. The subplots at the upper-right corner indicate the phase winding patterns of the modes.

Fig. 2.. Characterization of the bulk valley vortex states.

(A) Photograph of the sample, which consists of eight cubic cells in each direction. (B) Magnified picture displaying the details of the upper surface. (C) Measured spectrum at a bulk site. The gray region indicates the simulated bandgap. a.u., arbitrary units. (D to F) Fourier spectra of the acoustic fields at 7300 Hz excited by a point-like source placed at the center. We adopt three 2D cuts in the 3D momentum space that contain the six valleys. (G) Simplified illustration of the Bloch modes at the ${\mathrm{W}}_3^{+}$ valley. The four balls denote four neighboring cavities, with their colors representing the phases.

Fig. 3.. Observation of valley kink states.

(A) Photograph of the sample, which consists of two domains with opposite structural parameter Δ. The red dashes denote the 2D interface. (B) (001) surface BZ. The projections of ${\mathrm{W}}_1^{\pm }$ and ${\mathrm{W}}_2^{\pm }$ valleys are labeled by ${\overline{\mathrm{W}}}_1^{\pm }$ and ${\overline{\mathrm{W}}}_2^{\pm }$ , respectively. (C) Simulated dispersion for the structure in (A), with periodic boundary conditions imposed along x and y directions and the z direction terminated by hard walls. The red and blue bands correspond to states localized at the interface and the outer boundaries, respectively, while the gray bands are bulk bands. (D) Simulated eigenfrequency contour at 8000 Hz (gray curves) in the surface BZ. The arrows indicate the propagation directions of the kink states at the valleys. (E) Measured acoustic field distribution (absolute value of sound pressure) at 8000 Hz on the interface (left) and on the middle xz plane (right). The source is denoted by the speaker icon, and the interface is highlighted by a red dashed line. (F) Decay profile of the valley kink states. The gray, blue, and red curves correspond to theoretical, simulated, and measured results, respectively. (G) Comparison between the measured (color map) and simulated (red line) dispersion of the valley kink state.

Fig. 4.. Topological properties of valley kink states.

(A) Schematic of the topological propagation of valley kink states through a 90° bend. (B) Measured acoustic field distribution at 8000 Hz on the middle xz plane. The source is denoted by the speaker icon, and the interface is highlighted by a red dashed line. (C) Measured transmission spectra of valley kink states for straight (blue curve) and bent (red curve) interfaces. The gray region indicates the bandgap. (D) Schematic of the topological refraction of valley kink states into free space. (E) Fourier spectrum of the acoustic field (at 8000 Hz) at the interface. (F) Simulated (left) and measured (right) acoustic field distribution at 8000 Hz in free space in the xy plane (at the same height as the interface). The inset shows the phase matching diagram for the outcoupling process. (G) Schematic of the topological localization of valley kink states at the interface between the sample and a hard wall. (H) Measured acoustic field distribution at 8000 Hz on the interface. (I) Measured acoustic field distributions at 8000 Hz along the x-directional middle line on the interface under open (blue curve) and closed (red curve) boundaries at the outcoupling surface.

Fig. 5.. 3D valley-dependent beam splitting using all six valleys.

(A) Schematic of the 3D valley-dependent beam splitting. (B) (111) surface BZ. The projections of ${\mathrm{W}}_1^{\pm }$ , ${\mathrm{W}}_2^{\pm }$ , and ${\mathrm{W}}_3^{\pm }$ valleys are labeled by ${\overline{\mathrm{W}}}_1^{\pm }$ , ${\overline{\mathrm{W}}}_2^{\pm }$ , and ${\overline{\mathrm{W}}}_3^{\pm }$ , respectively. (C) Simulated eigenfrequency contour for the (111) interface at 8000 Hz (gray curve) in the surface BZ. The arrows indicate the propagation directions of the kink states at the valleys. (D to F) Measured acoustic field distributions at 8000 Hz in the corresponding planes for the outcoupling waves of the six valleys.