Bursting gamma oscillations in neural mass models

Abstract

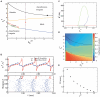
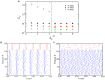
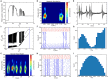
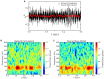
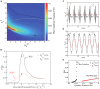
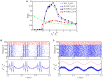
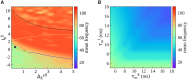
Gamma oscillations (30-120 Hz) in the brain are not periodic cycles, but they typically appear in short-time windows, often called oscillatory bursts. While the origin of this bursting phenomenon is still unclear, some recent studies hypothesize its origin in the external or endogenous noise of neural networks. We demonstrate that an exact neural mass model of excitatory and inhibitory quadratic-integrate and fire-spiking neurons theoretically predicts the emergence of a different regime of intrinsic bursting gamma (IBG) oscillations without any noise source, a phenomenon due to collective chaos. This regime is indeed observed in the direct simulation of spiking neurons, characterized by highly irregular spiking activity. IBG oscillations are distinguished by higher phase-amplitude coupling to slower theta oscillations concerning noise-induced bursting oscillations, thus indicating an increased capacity for information transfer between brain regions. We demonstrate that this phenomenon is present in both globally coupled and sparse networks of spiking neurons. These results propose a new mechanism for gamma oscillatory activity, suggesting deterministic collective chaos as a good candidate for the origin of gamma bursts.

Keywords: bursting; gamma oscillations; neural mass model; phase amplitude coupling; spiking neural network (SNN); synchronization.

Figure 1

(A) Phase diagram for external drive $I_0^E$ and heterogeneity ${\text{Δ}}_E^{eff}$ obtained from the deterministic neural mass model. The blue line represents the supercritical Hopf bifurcation line separating a stable fixed point (asynchronous irregular in the network) from a stable limit cycle (PING oscillations in the network). The green line separates the stable fixed point and the chaotic region (IBG regime). The red line represents a period-doubling bifurcation and thus separates the chaotic region from the limit cycle region. The dark-yellow line represents a subcritical Hopf bifurcation, giving rise to the coexistence of asynchronous irregular dynamics and PING oscillations. Finally, the black line is a saddle-node of limit cycles separating the bistable region from a stable fixed point (B). Top panel: average membrane potential for excitatory (inhibitory) neurons V^E (V^I) in blue (red) from network simulations (continuous line) and neural mass model (line with filled circles) at the point indicated on the phase diagram as red star (${\text{Δ}}_E^{eff}=2.0$, $I_0^E=2.0$). Bottom panel: the corresponding raster plot for the excitatory and inhibitory neurons. D represents the delay in the synchronization of spike times between excitatory and inhibitory neurons. (C) The bifurcation diagram obtained with the software X-Windows PhasePlane plus Auto (XPPAUT) along the dashed line indicated in (A). The red line represents stable fixed points, the green line is a stable limit cycle, and the blue line is an unstable limit cycle. (D) The CV of spiking neurons from the network simulation with respect to external drive $I_0^E$ and population heterogeneity Γ_E (in these simulations Δ_E = 0, so ${\text{Δ}}_E^{eff}={\text{Γ}}_E$). Notice that the CV depends on initial conditions (random in these simulations) in the bistable regime; that is why we observe a higher CV for oscillatory solutions and a lower CV for asynchronous solutions. (E) The delay D, at the same point indicated by the star in the phase diagram, concerns the variation of the synaptic strength between excitatory and inhibitory synapses, obtained from the neural mass model.

Figure 2

(A) Oscillations' amplitude Σ_V, obtained by performing adiabatic simulations by first increasing (right triangles) and then decreasing (left triangles) ${\text{Δ}}_E^{eff}$ at $I_0^E=5.0$. Here Δ_E = 0, and we use Cauchy noise of amplitude ${\text{Γ}}_E={\text{Δ}}_E^{eff}$. Various network sizes N have been employed, as indicated in the legend. We observe that Σ_V goes to zero by increasing N in the asynchronous regimes and does not depend on N in the oscillatory regime. The dashed vertical line represents the saddle-node bifurcation point indicated by the black square in Figure 1A, obtained from the neural mass model. (B, C) Show the raster plot obtained for Γ_E = 2.0, indicating the coexistence of asynchronous and PING oscillations depending on the initial conditions.

Figure 3

(A) The real part of the first Lyapunov exponent in the function of $I_0^E$. (B) Bifurcation diagram of the chaotic region generated by plotting the maximum value of the instantaneous firing rate R^E obtained from mean-field simulations. The blue vertical asymptote on the left is the limit point separating the asynchronous and the chaotic regions, while the vertical asymptote on the right is the point where the first period-doubling bifurcation appears. (C) A power spectrogram obtained from the neural mass model. (D) Power spectrogram of the mean voltage [presented in (E)]. (E) Time traces of the mean voltage of excitatory populations. (F) Raster plot of network simulations. We ordered the neurons according to their coefficient of variation, cv_i. Blue dots represent the excitatory neurons, and red dots are inhibitory neurons. (G) Histogram of the coefficient of variation (CV) across neurons for the simulation of (F). (H) Raster plot of network simulations for the same parameters as (E) but with Cauchy noise instead of heterogeneity. (I) CV for the simulation of (H). In all panels, $I_0^E=0.5$ and ${\text{Δ}}_{eff}^E=0.4$. (D–G) are for heterogeneous networks (${\text{Δ}}_{eff}^E={\text{Δ}}_E=0.4$ and Γ_E = 0), and (H, I) are for networks with Cauchy noise (${\text{Δ}}_{eff}^E={\text{Γ}}_E=0.4$ and Δ_E = 0). The values of the power spectrogram < 10⁻¹ are set to 10⁻¹ for (C, D).

Figure 4

(A) Time traces of the mean voltage of excitatory neurons ($I_0^E=-3.0,{\text{Γ}}_E={\text{Δ}}_E^{eff}=3.0$) for a network of N = 16, 000 neurons—close to the Hopf bifurcation line (see Figure 1A). The black line represents the voltage from the network simulation, and the red line represents the same from the neural mass model with additive Gaussian noise (see Section 2). The spectrogram of the corresponding signal from network simulation and the neural mass model are plotted in (B, C). The values of the power spectrogram < 10⁻⁵ are set to 10⁻⁵ for (B, C).

Figure 5

(A) Phase-amplitude coupling (PAC) to the external θ forcing of amplitude A = 0.04 vs. the external drive $I_0^E$ and the heterogeneity ${\text{Δ}}_E^{eff}$. This is a heat map of Figure 1A in the parameter space, and the IBG is inside the red circle lines around the orange dot, as in Figure 1A. (B) PAC value vs. the distance to the critical value of the external drive ($I_0^E-I_0^{Ec}$) at the two different population heterogeneities, ${\text{Δ}}_E^{eff}=0.4$ (black line) and ${\text{Δ}}_E^{eff}=6.0$ (red line). For the Hopf bifurcation (${\text{Δ}}_E^{eff}=6.0$), $I_0^{Ec}=-2.88$, while for the bifurcation to chaos (${\text{Δ}}_E^{eff}=0.4$), $I_0^{Ec}=0.47$. (C) Time traces of the mean excitatory voltage (black line) were obtained at the point represented by a dark-yellow circle in (A) (${\text{Δ}}_E^{eff}=0.4$, $I_0^E=0.35$). The red line represents the external theta drive. (D) The time traces of mean excitatory voltage and external theta drive at the state point are represented by the dark green circle (${\text{Δ}}_E^{eff}=6.0$, $I_0^E=-3.0$). (E) PAC vs. the real part of the maximum of Lyapunov exponent λ for different values of $I_0^E$ at two values of ${\text{Δ}}_E^{eff}$ (${\text{Δ}}_E^{eff}=0.4$ and ${\text{Δ}}_E^{eff}=8.0$). Data were obtained from the neural mass model. The amplitude of the external θ forcing signal is A = 0.04 for (A, E) and the amplitude is A = 0.2 for (B–D).

Figure 6

(A) Phase-amplitude coupling (PAC) to the external θ forcing of amplitude A = 0.2 vs. the distance to the critical value of the external drive ($I_0^E-I_0^{Ec}$) at two different population heterogeneity levels for sparse networks (same values as in Figure 5B, Γ_E = 0.4 and Γ_E = 6.0). The dashed line with solid circles represents the PAC values for different in-degree K. (B) Top panel: raster plot from network simulation [see black circle in (A), Γ_E = 0.4, $I_0^E=0.35$]. Bottom panel: the corresponding time traces for the mean membrane potential for the excitatory population (blue) and the external theta drive $I_0^{\theta }$ (red). (C) The same as for (B), but at the point indicated by the red circle in (A) (Γ_E = 6.0, $I_0^E=-3.0$).

Figure 7

(A) Dependence of oscillations' frequency on external drive $I_0^E$ and neural heterogeneity ${\text{Δ}}_E^{eff}$. The frequency of oscillations is estimated as the mean of the power spectrum of the mean membrane potential of the excitatory population V^E(t). This is a heat map of Figure 1A in the parameter space. (B) Oscillations' frequency as a function of the intrinsic membrane time constant of excitatory and inhibitory neurons (${\tau }_m^E$ and ${\tau }_m^I$) within the bursting region [indicated by the solid black circle in (A)].