Statistical Mechanical Theories of Membrane Permeability
- PMID: 39283709
- PMCID: PMC11701864
- DOI: 10.1021/acs.jpcb.4c05020
Statistical Mechanical Theories of Membrane Permeability
Abstract
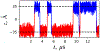
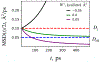
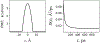
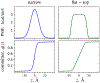
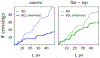
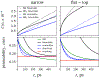
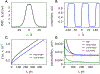
A popular theoretical framework to compute the permeability coefficient of a molecule is provided by the classic Smoluchowski-Kramers treatment of the steady-state diffusive flux across a free-energy barrier. Within this framework, commonly termed "inhomogeneous solubility-diffusion" (ISD), the permeability, P, is expressed in closed form in terms of the potential of mean force and position-dependent diffusivity of the molecule of interest along the membrane normal. In principle, both quantities can be calculated from all-atom MD simulations. Although several methods exist for calculating the position-dependent diffusivity, each of these is at best an estimate. In addition, the ISD model does not account for memory effects along the chosen reaction coordinate. For these reasons, it is important to seek alternative theoretical formulations to determine the permeability coefficient that are able to account for the factors ignored by the ISD approximation. Using Green-Kubo linear response theory, we establish the familiar constitutive relation between the flux density across the membrane and the difference in the concentration of a permeant molecule, j = PΔC. On this basis, we derive a time-correlation function expression for the nonequilibrium flux across a membrane that is reminiscent of the transmission coefficient in the reactive flux formalism treatment of transition rates. An analysis based on the transition path theory framework is exploited to derive alternative expressions for the permeability coefficient. The different strategies are illustrated with stochastic simulations based on the generalized Langevin equation in addition to unbiased molecular dynamics simulations of water permeation of a lipid bilayer.
Figures
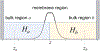

Similar articles
-
Two Relations to Estimate Membrane Permeability Using Milestoning.J Phys Chem B. 2016 Aug 25;120(33):8606-16. doi: 10.1021/acs.jpcb.6b02814. Epub 2016 May 27. J Phys Chem B. 2016. PMID: 27154639 Free PMC article.
-
Generalized Langevin Methods for Calculating Transmembrane Diffusivity.J Chem Theory Comput. 2016 Nov 8;12(11):5609-5619. doi: 10.1021/acs.jctc.6b00747. Epub 2016 Oct 12. J Chem Theory Comput. 2016. PMID: 27673448
-
Subdiffusion in Membrane Permeation of Small Molecules.Sci Rep. 2016 Nov 2;6:35913. doi: 10.1038/srep35913. Sci Rep. 2016. PMID: 27805049 Free PMC article.
-
Molecular simulation of nonfacilitated membrane permeation.Biochim Biophys Acta. 2016 Jul;1858(7 Pt B):1672-87. doi: 10.1016/j.bbamem.2015.12.014. Epub 2015 Dec 17. Biochim Biophys Acta. 2016. PMID: 26706099 Review.
-
Permeability across lipid membranes.Biochim Biophys Acta. 2016 Oct;1858(10):2254-2265. doi: 10.1016/j.bbamem.2016.03.032. Epub 2016 Apr 14. Biochim Biophys Acta. 2016. PMID: 27085977 Review.
Cited by
-
Permeability Benchmarking: Guidelines for Comparing in Silico, in Vitro, and in Vivo Measurements.J Chem Inf Model. 2025 Feb 10;65(3):1067-1084. doi: 10.1021/acs.jcim.4c01815. Epub 2025 Jan 17. J Chem Inf Model. 2025. PMID: 39823383 Free PMC article. Review.
References
-
- Rashid M; Malik MY; Singh SK; Chaturvedi S; Gayen JR; Wahajuddin M Bioavailability enhancement of poorly soluble drugs: the holy grail in pharma industry. Curr. Pharm. Design 2019, 25, 987–1020. - PubMed
-
- Tse CH; Comer J; Wang Y; Chipot C Link between membrane composition and permeability to drugs. J. Chem. Theory Comput 2018, 14, 2895–2909. - PubMed
-
- Loverde SM Molecular simulation of the transport of drugs across model membranes. J. Phys. Chem. Lett 2014, 5, 1659–1665. - PubMed
-
- Smoluchowski M Drei vorträge über diffusion, brownsche molekularbewegung und koagulation von kolloidteilchen. Phys. Z 1916, 17, 557–571.
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

