Bayesian Calibration to Address the Challenge of Antimicrobial Resistance: A Review
- PMID: 39286062
- PMCID: PMC7616450
- DOI: 10.1109/ACCESS.2024.3427410
Bayesian Calibration to Address the Challenge of Antimicrobial Resistance: A Review
Abstract
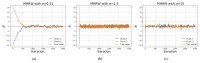
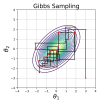
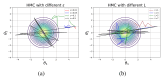
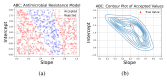
Antimicrobial resistance (AMR) emerges when disease-causing microorganisms develop the ability to withstand the effects of antimicrobial therapy. This phenomenon is often fueled by the human-to-human transmission of pathogens and the overuse of antibiotics. Over the past 50 years, increased computational power has facilitated the application of Bayesian inference algorithms. In this comprehensive review, the basic theory of Markov Chain Monte Carlo (MCMC) and Sequential Monte Carlo (SMC) methods are explained. These inference algorithms are instrumental in calibrating complex statistical models to the vast amounts of AMR-related data. Popular statistical models include hierarchical and mixture models as well as discrete and stochastic epidemiological compartmental and agent based models. Studies encompassed multi-drug resistance, economic implications of vaccines, and modeling AMR in vitro as well as within specific populations. We describe how combining these topics in a coherent framework can result in an effective antimicrobial stewardship. We also outline recent advancements in the methodology of Bayesian inference algorithms and provide insights into their prospective applicability for modeling AMR in the future.
Keywords: Antimicrobial resistance; Bayesian inference; Markov chain Monte Carlo; antimicrobial stewardship; approximate Bayesian computation; epidemiology; sequential Monte Carlo.
Figures

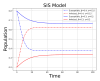
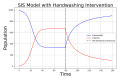
References
-
- Ferreira D, Barthoulot M, Pottecher J, Torp KD, Diemunsch P, Meyer N. Theory and practical use of Bayesian methods in interpreting clinical trial data: A narrative review. Brit J Anaesthesia. 2020 Aug;125(2):201–207. - PubMed
-
- Gelman A, Rubin DB. Markov chain Monte Carlo methods in biostatistics. Stat Methods Med Res. 1996 Dec;5(4):339–355. - PubMed
-
- Antimicrobial Resistance. 2023. [Accessed: Jul. 3, 2023]. [Online]. Available: https://www.who.int/news-room/fact-sheets/detail/antimicrobial-resistance.
-
- Abel K, Dark P, Felton T, Ustianowski A, Van Staa T, Wilson P, Bower P. System-wide approaches to antimicrobial therapy and antimicrobial resistance in the U.K.: The AMR-X framework. Lancet Microbe. 2024;5(5):e500–e507. - PubMed
LinkOut - more resources
Full Text Sources
Miscellaneous
