Mathematical Models of Ocular Drug Delivery

Abstract

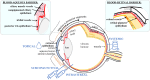
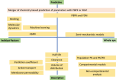
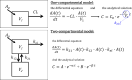
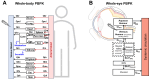
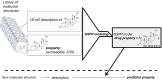
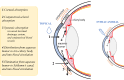
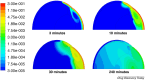
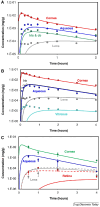
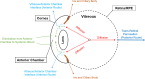
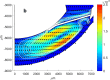
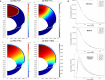
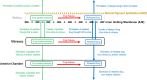
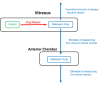
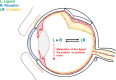
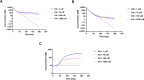
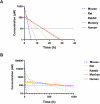
Drug delivery is an important factor for the success of ocular drug treatment. However, several physical, biochemical, and flow-related barriers limit drug exposure of anterior and posterior ocular target tissues during drug treatment via topical, subconjunctival, intravitreal, or systemic routes. Mathematical models encompass various barriers so that their joint influence on pharmacokinetics (PKs) can be simulated in an integrated fashion. The models are useful in predicting PKs and even pharmacodynamics (PDs) of administered drugs thereby fostering development of new drug molecules and drug delivery systems. Furthermore, the models are potentially useful in interspecies translation and probing of disease effects on PKs. In this review article, we introduce current modeling methods (noncompartmental analyses, compartmental and physiologically based PK models, and finite element models) in ocular PKs and related drug delivery. The roles of top-down models and bottom-up simulations are discussed. Furthermore, we present some future challenges, such as modeling of intra-tissue distribution, prediction of drug responses, quantitative systems pharmacology, and possibilities of artificial intelligence.

Figure 1.

A schematic representation of the ocular anatomy, blood-aqueous barrier, blood-retinal barrier, and selected routes of ocular drug administration.

Figure 2.

Classification of model types. Individual factors (e.g. receptor affinity and membrane permeability) can be used as parameters in models. Clearance, volume of distribution and half-life are pharmacokinetic parameters that depend on binding and partitioning (affects volume and half-life) and permeability and active transport (affects clearance and half-life). Machine learning methods correlate parameter values with chemical structure, thereby providing predictions. Likewise, quantitative structure property relationship (QSPR) models generate such correlations. Docking and molecular dynamics and other molecular modeling tools are used for molecular level processes, such as receptor binding. Pharmacokinetic models integrate various factors even at the level of whole eye providing descriptive and predictive information.

Figure 3.

Schematic representation of modelling dynamics. Descriptive models of in vivo data provide pharmacokinetic parameters that can be further used as components in the bottom-up predictive models. Such models can utilize also individual parameters that are based on in vitro assays and in silico models. Modeling can be further extended to pharmacodynamics by adding response related parameters and linking them to pharmacokinetics in the effect compartment. Quantitative systems pharmacology aims to incorporate also complex biochemical systems biological pathways to the models.

Figure 4.

Schematic representation of the one- and two-compartment models after bolus injection. The differential and final solved equations are shown, where A_o is the injected dose, CL is the clearance, and V is the volume of distribution in the compartment, 1 = central compartment, 2 = peripheral compartment, k_el = constant rate of elimination form the central compartment, k₁₂ = transfer rate constant from the central to the peripheral compartment, k₂₁ = transfer rate constant from the peripheral to the central compartment. C is the concentration in the central compartment at any time point, C₀ is the initial concentration (at time 0), and the sum of A and B in the two-compartmental model, α correspond to the slope of the initial-phase decline in semi-logarithm plot, and β to the terminal-phase, and both relate to the micro-constants (e.g. α + β = k₁₂ + k₂₁ + k_el) in the two-compartmental model.

Figure 5.

Schematic representation of the several components of a population model: structural, statistic, and covariate models using the example of CL of one-compartment model after intravitreal injection (the same applies to V1; adapted from Ref. 20). The statistical model describes the variability in the observed data, η_indv (intersubject variability) accounts for the difference between an individual's parameter value and the population value, ε (residual or unexplained intrasubject variability) describes the difference between the observed data for the individual and the model prediction at each time point. The covariate model shows a property of the subject (weight) which explains part of the variability in the CL parameter. The statistical and covariate models add the influence of the various sources of variability for the estimation of the population predicted concentration (C_{pop pred}) and individual predictive concentrations (C_{indv. pred}).

Figure 6.

Schematic examples of PBPK models. (A) In whole body PBPK models the drug is distributed to the tissues by blood flow (Q) and eliminated from tissues by clearances (CL; e.g. renal excretion and hepatic metabolism). Drug partitioning from the arterial blood flow to the tissues is determined by membrane permeability and tissue/blood distribution coefficients. (B) Scheme of a simple PBPK model for intravitreal injection of a protein drug. SA, surface area; P_RPE, permeability across retinal pigment epithelium.

Figure 7.

Overview of the finite element model (FEM) illustrating a geometrically accurate eye model divided in 36,613 mesh elements, the equations governing the transport of macromolecules via diffusion and convection, and the calculated macromolecule concentrations in the vitreous (blue), retina, and aqueous humor (light blue) after intravitreal injection (purple). The transport of macromolecules in the vitreous and the retina is driven by diffusion, whereas convection dominates in the aqueous humor. Convection was set to zero in the retina. D is the diffusion coefficient (m² s⁻¹), k_B is the Boltzmann constant (1.381 × 10⁻²³ J K⁻¹), T is the absolute temperature (310.15 K), η is the dynamic viscosity (0.00069 kg m⁻¹ s⁻¹), r_H is the hydrodynamic radius of the molecule (m), P_app is the apparent permeability (m s⁻¹), h is the thickness of the layer (m), and K is the retina/vitreous partition coefficient (0.5). From Lamminsalo et al.

Figure 8.

Basic scheme of QSPR modelling. The models find correlation between molecular descriptors and pharmacological property (e.g. receptor binding affinity, permeability, clearance, and metabolic reaction). The model can then be used to predict the property for new compounds based on structure, even before the compounds are synthesized. When the relationship between a set of descriptors and a given response is weak or highly nonlinear, it may be possible to create a useful classification model.

Figure 9.

Pharmacokinetic processes involved in topical ocular drug administration. Drug loss by solution drainage and systemic absorption through the conjunctiva limit the contact time of the instilled drug to a few minutes on the ocular surface. Drug absorption takes place via the cornea and conjunctiva. The conjunctiva is about nine times more permeable than the cornea, but the major part of conjunctivally absorbed drug is lost to the systemic blood circulation and not distributed to the inner eye. Drug elimination from the anterior chamber is governed by aqueous humor outflow (approximately 3 µL/min) and blood flow of the iris-ciliary body (clearance even 30 µL/min). Intracameral injection data are needed to determine drug clearance from the anterior chamber and volume of drug distribution. Furthermore, AUC values of drug in the aqueous humor after intracameral and topical administration are used to determine topical ocular drug bioavailability. Unfortunately, ocular bioavailability (range of 0.1–5%) has been calculated only for less than 10 compounds.

Figure 10.

Simulated intraocular moxifloxacin concentrations at different times after eye drop instillation. Drug concentrations within ocular tissues are clearly discerned.^,

Figure 11.

Concentration profiles for topically administered (A) pilocarpine nitrate (0.27%, 25 µL), (B) timolol maleate (0.65%, 25 µL), and (C) moxifloxacin hydrochloride (0.3%, 30 µL) in ocular tissues. Simulated concentrations are shown as lines, and corresponding experimental data as circles. The CFD model predicts well drug concentrations in the cornea, aqueous humor, and iris-ciliary body, but the predicted drug concentrations in the posterior segment are less accurate. Reproduced from Refs. , .

Figure 12.

Mechanistic model of intravitreal pharmacokinetics based on the vitreal diffusion and trans retinal permeability of compounds.^, The lens does not allow trans-lenticular permeation. Anterior elimination takes place only through the limited space between the ciliary body, iris, and lens via the posterior chamber to the anterior chamber. Drugs are eliminated from the aqueous humor by outflow and permeation to the circulation of the anterior uvea.

Figure 13.

Comparison of calculated vitreal clearance of fluorescein, sucrose, and ranibizumab with the experimental data of various molecules with wide size range. The original references are found in a previous publication. Clearance of the three model molecules were calculated from the vitreal elimination constants as CL = V/k_v, where V is the volume of drug distribution (1.5 mL).

Figure 14.

The aqueous humor flow is enhanced with a temperature gradient, heat transfer, and gravity. This generates a circulatory flow in the anterior chamber, improves drug mixing in the aqueous humor, and leads to faster and more realistic drug elimination. From Lamminsalo et al.

Figure 15.

(A) Antibody concentration profiles predicted by Lamminsalo's CFD model at 0, 0.3, 3, and 30 days after intravitreal administration. An apparent initial distribution volume of 400 µL and intraocular pressure of 10.1 Torr were used. At day 30, the highest antibody concentration is about 200 times less than at day 0. (B) The simulated concentration profiles in the vitreous, retina, and aqueous humor are shown as lines, and corresponding experimental data as circles.

Figure 16.

Schematic illustrating the pharmacokinetics of intravitreal nano- and microparticles. These formulations typically release drug in the vitreous, while being eliminated at the same time.

Figure 17.

Simulated kinetics of released drug in the vitreous after intravitreal injection of particles with elimination half-lives of 1 week (A) and 4 weeks (B). Three different first-order release rates (release half-lives 1, 4, and 8 weeks) were simulated and the elimination half-life of the free drug was 3 hours. The volume of drug distribution was considered to be the anatomic volume of the vitreous humor.

Figure 18.

Compartmental model of an intravitreal implant. The implant releases the drug with zero-order or first-order kinetics in the vitreous. The released corticosteroids are eliminated via the posterior and anterior routes.

Figure 19.

Schematic model of intravitreal pharmacokinetics involving drug binding to the vitreous. The scheme assumes that there is a single binding site.

Figure 20.

Influence of vitreal binding affinity (K_d 1, 10, 100, and 1000 µM) on drug concentration in the human vitreous (volume 4.5 mL). The assumed drug was a macromolecule (MW = 100 kDa) and elimination half-life was 8 days for free drug. The dose was 20 µmol and the anatomic volume of human vitreous was assumed to be 4.5 mL. The binding capacity of the vitreous (B_max) was 125 µM. (A) The total concentration of the drug in the vitreous. (B) Concentration of free drug in the vitreous. (C) Elimination half-life of total concentration in the vitreous.

Figure 21.

Single dose intravitreal kinetics of (A) fluorescein and (B) FITC-dextran (150 kDa) in the eyes of different species. The doses result in similar compound exposure (AUC), but different profiles in various species. The black dotted lines show an assuming effective concentration of 10 µM (A) and 100 nM (B) for small and macromolecules, respectively.