Using neural networks for image analysis in general physiology
- PMID: 39287612
- PMCID: PMC11410919
- DOI: 10.1085/jgp.202413623
Using neural networks for image analysis in general physiology
Abstract
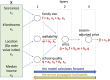
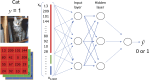
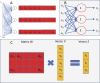
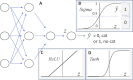
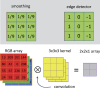
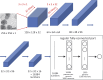
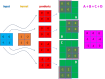
An article with three goals, namely, to (1) provide the set of ideas and information needed to understand, at a basic level, the application of convolutional neural networks (CNNs) to analyze images in biology; (2) trace a path to adopting and adapting, at code level, the applications of machine learning (ML) that are freely available and potentially applicable in biology research; (3) by using as examples the networks described in the recent article by Ríos et al. (2024. https://doi.org/10.1085/jgp.202413595), add logic and clarity to their description.
© 2024 Rios.
Conflict of interest statement
Disclosures: The author declares no competing interests exist.
Figures


Similar articles
-
Machine Learning Algorithms in Neuroimaging: An Overview.Acta Neurochir Suppl. 2022;134:125-138. doi: 10.1007/978-3-030-85292-4_17. Acta Neurochir Suppl. 2022. PMID: 34862537 Review.
-
Application of Convolutional Neural Networks for Automated Ulcer Detection in Wireless Capsule Endoscopy Images.Sensors (Basel). 2019 Mar 13;19(6):1265. doi: 10.3390/s19061265. Sensors (Basel). 2019. PMID: 30871162 Free PMC article.
-
Generative and discriminative model-based approaches to microscopic image restoration and segmentation.Microscopy (Oxf). 2020 Apr 8;69(2):79-91. doi: 10.1093/jmicro/dfaa007. Microscopy (Oxf). 2020. PMID: 32215571 Free PMC article. Review.
-
Visualization Methods for Image Transformation Convolutional Neural Networks.IEEE Trans Neural Netw Learn Syst. 2019 Jul;30(7):2231-2243. doi: 10.1109/TNNLS.2018.2881194. Epub 2018 Dec 11. IEEE Trans Neural Netw Learn Syst. 2019. PMID: 30561353
-
CellProfiler Analyst 3.0: accessible data exploration and machine learning for image analysis.Bioinformatics. 2021 Nov 5;37(21):3992-3994. doi: 10.1093/bioinformatics/btab634. Bioinformatics. 2021. PMID: 34478488 Free PMC article.
References
-
- Abadi, M., Barham P., Chen J., Chen Z., Davis A., Dean J., Devin M., Ghemawat S., Irving G., Isard M., et al. . 2016. TensorFlow: A system for large-scale machine learning. arXiv. 10.48550/arXiv.1605.08695 (Preprint posted May 30, 2016). - DOI
-
- Baylor, S. 2021. Computational Cell Physiology. Second edition. Self-published, Chicago, IL, USA. p. 518.
-
- Csurka, G., Volpi R., and Chidlovskii B.. 2023. Semantic image segmentation: Two decades of research. arXiv. 10.48550/arXiv.2302.06378 (Preprint posted February 13, 2023). - DOI
-
- Ham, D., Park H., Hwang S., and Kim K.. 2021. Neuromorphic electronics based on copying and pasting the brain. Nat. Electron. 4:635–644. 10.1038/s41928-021-00646-1 - DOI
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

