Integrating local energetics into Maxwell-Calladine constraint counting to design mechanical metamaterials
- PMID: 39294968
- PMCID: PMC11773508
- DOI: 10.1103/PhysRevE.110.025002
Integrating local energetics into Maxwell-Calladine constraint counting to design mechanical metamaterials
Abstract
The Maxwell-Calladine index theorem plays a central role in our current understanding of the mechanical rigidity of discrete materials. By considering the geometric constraints each material component imposes on a set of underlying degrees of freedom, the theorem relates the emergence of rigidity to constraint counting arguments. However, the Maxwell-Calladine paradigm is significantly limited-its exclusive reliance on the geometric relationships between constraints and degrees of freedom completely neglects the actual energetic costs of deforming individual components. To address this limitation, we derive a generalization of the Maxwell-Calladine index theorem based on susceptibilities that naturally incorporate local energetic properties such as stiffness and prestress. Using this extended framework, we investigate how local energetics modify the classical constraint counting picture to capture the relationship between deformations and external forces. We then combine this formalism with group representation theory to design mechanical metamaterials where differences in symmetry between local energy costs and structural geometry are exploited to control responses to external forces.
Figures
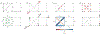
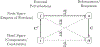

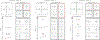
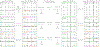
References
-
- Clerk Maxwell J, “On the calculation of the equilibrium and stiffness of frames,” The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 27, 294–299 (1864).
-
- Calladine CR, “Buckminster fuller’s “tensegrity” structures and clerk maxwell’s rules for the construction of stiff frames,” International Journal of Solids and Structures 14, 161–172 (1978).
-
- Lubensky TC Kane CL, Mao Xiaoming, Souslov A, and Sun Kai, “Phonons and elasticity in critically coordinated lattices,” Reports on Progress in Physics 78, 073901 (2015). - PubMed
-
- Phillips JC, “Topology of covalent non-crystalline solids ii: Medium-range order in chalcogenide alloys and asi(ge),” Journal of Non-Crystalline Solids 43, 37–77 (1981).
-
- Boolchand P, Lucovsky G, Phillips JC, and Thorpe MF, “Self-organization and the physics of glassy networks,” Philosophical Magazine 85, 3823–3838 (2005).
Grants and funding
LinkOut - more resources
Full Text Sources
