CHARMM at 45: Enhancements in Accessibility, Functionality, and Speed
- PMID: 39303207
- PMCID: PMC11492285
- DOI: 10.1021/acs.jpcb.4c04100
CHARMM at 45: Enhancements in Accessibility, Functionality, and Speed
Abstract
Since its inception nearly a half century ago, CHARMM has been playing a central role in computational biochemistry and biophysics. Commensurate with the developments in experimental research and advances in computer hardware, the range of methods and applicability of CHARMM have also grown. This review summarizes major developments that occurred after 2009 when the last review of CHARMM was published. They include the following: new faster simulation engines, accessible user interfaces for convenient workflows, and a vast array of simulation and analysis methods that encompass quantum mechanical, atomistic, and coarse-grained levels, as well as extensive coverage of force fields. In addition to providing the current snapshot of the CHARMM development, this review may serve as a starting point for exploring relevant theories and computational methods for tackling contemporary and emerging problems in biomolecular systems. CHARMM is freely available for academic and nonprofit research at https://academiccharmm.org/program.
Conflict of interest statement
The authors declare the following competing financial interest(s): Alexander D. MacKerell, Jr. is Co-founder and CSO of SilcsBio LLC.
Figures



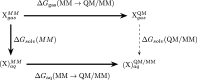
References
-
- Macuglia D.; Roux B.; Ciccotti G. The emergence of protein dynamics simulations: how computational statistical mechanics met biochemistry. Euro. Phys. J. H 2022, 47, 13.10.1140/epjh/s13129-022-00043-y. - DOI
-
- Brooks B. R.; Bruccoleri R. E.; Olafson B. D.; States D. J.; Swaminathan S.; Karplus M. CHARMM - a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983, 4, 187–217. 10.1002/jcc.540040211. - DOI
Publication types
MeSH terms
Grants and funding
- R35 GM148261/GM/NIGMS NIH HHS/United States
- R01 GM046736/GM/NIGMS NIH HHS/United States
- S10 OD034346/OD/NIH HHS/United States
- R01 GM039478/GM/NIGMS NIH HHS/United States
- R01 GM135392/GM/NIGMS NIH HHS/United States
- R01 GM140316/GM/NIGMS NIH HHS/United States
- R35 GM133754/GM/NIGMS NIH HHS/United States
- R01 GM132481/GM/NIGMS NIH HHS/United States
- R01 GM138472/GM/NIGMS NIH HHS/United States
- R01 GM129519/GM/NIGMS NIH HHS/United States
- R35 GM126948/GM/NIGMS NIH HHS/United States
- R35 GM141930/GM/NIGMS NIH HHS/United States
- R35 GM131710/GM/NIGMS NIH HHS/United States
- ZIA HL000340/ImNIH/Intramural NIH HHS/United States
- R21 GM148895/GM/NIGMS NIH HHS/United States
- R01 GM143810/GM/NIGMS NIH HHS/United States
- ZIA HL001051/ImNIH/Intramural NIH HHS/United States
- Z01 HL001052/ImNIH/Intramural NIH HHS/United States

