Interlimb coordination is not strictly controlled during walking

Abstract

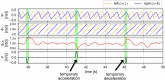
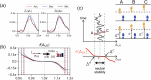
In human walking, the left and right legs move alternately, half a stride out of phase with each other. Although various parameters, such as stride frequency and length, vary with walking speed, the antiphase relationship remains unchanged. In contrast, during walking in left-right asymmetric situations, the relative phase shifts from the antiphase condition to compensate for the asymmetry. Interlimb coordination is important for adaptive walking and we expect that interlimb coordination is strictly controlled during walking. However, the control mechanism remains unclear. In the present study, we derived a quantity that models the control of interlimb coordination during walking using two coupled oscillators based on the phase reduction theory and Bayesian inference method. The results were not what we expected. Specifically, we found that the relative phase is not actively controlled until the deviation from the antiphase condition exceeds a certain threshold. In other words, the control of interlimb coordination has a dead zone like that in the case of the steering wheel of an automobile. It is conjectured that such forgoing of control enhances energy efficiency and maneuverability. Our discovery of the dead zone in the control of interlimb coordination provides useful insight for understanding gait control in humans.

Fig. 1. Schematic diagram of the study.

a Measurement of the leg motion, represented by φ_i(t) (i ∈ (L, R)), during walking on a treadmill with a perturbation in the belt speed, represented by p(t). b Two coupled limit-cycle oscillators with phases ϕ_i(t) (i ∈ (L, R)) whose dynamics are described by phase equations with phase coupling functions Γ_ij(ϕ_j − ϕ_i), phase sensitivity functions Z_i(ϕ_i), external perturbation I(t), and Gaussian noise ξ_i ((i, j) = (L, R), (R, L)). c Integration of the measured data and phase equations to derive the dynamics of the relative phase Δ_LR, which reflects the control of interlimb coordination. When Δ_LR = π, corresponding to B, the legs move in an exactly alternating manner. As Δ_LR moves away from π, the deviation from this antiphase relationship increases (see A and C, with Δ_LR = Δ^A and Δ^C). If the interlimb coordination is strictly controlled to maintain the antiphase relationship, the function f(Δ_LR), which describes the control of interlimb coordination, should intersect the horizontal axis at π with a steep negative slope.

Fig. 2. Measured and reconstructed time series for one representative subject (Subject G) under mixed conditions.

The leg motion, represented by φ_i(t) (i ∈ (L, R)), measured during walking was transformed to the oscillator phases ϕ_i(t) (i ∈ (L, R)), from which we obtain the relative phase Δ_LR. The disturbance of the treadmill belt speed from 1.0 m/s is represented as p(t). The green regions indicate the times at which temporary acceleration or deceleration is applied to the treadmill belt speed.

Fig. 3. Results for the control of interlimb coordination for one representative subject (Subject G).

a Phase sensitivity functions Z_i(ϕ_i) (i ∈ (L, R)) for acceleration (Acc), deceleration (Dec), and mixed (Mix) conditions. b Control of interlimb coordination, represented by f(Δ_LR). The vertical dotted lines indicate 3 standard deviations from the mean of the observed Δ_LR. In the region outside the vertical dotted line, the estimated function f(Δ_LR) is displayed in pale color. The function f(Δ_LR) is shifted in order to place the mean of the observed values of Δ_LR at π to improve visualization. The histogram displays the noise intensity, σ_LR. (An expanded histogram, with values 30 times larger than the actual values, is also given.) The mean and standard deviation of the derived noise intensity for all results are 0.0106π and 0.0021π, respectively. These values are too small to cause deviation of Δ_LR from the flat region of f(Δ_LR). c A schematic diagram for the interpretation of f(Δ_LR). The flat region near Δ_LR = π at B (neutral stability) and the steep negative slope in the regions away from π reflect the fact that the relative phase between the legs is not actively controlled until the deviation from π exceeds a threshold (Δ^A − π at A and Δ^C − π at C), where motion of the legs deviates significantly from the antiphase relationship.

Fig. 4. Characteristics of the control of interlimb coordination, represented by f(Δ_LR).

a Approximation of f(Δ_LR) by a piecewise linear function within 3 standard deviations (3SD) (vertical dotted lines) from the mean of the observed Δ_LR. The quantity l_C is the length of the flat region in which we have f(Δ_LR) = 0, and g_L and g_R are the slopes in the left and right outside regions, respectively. The three parameters l_C, g_L, and g_R were determined by the left and right endpoints of the flat region (white circles) such that the discrepancy between the original and approximated functions is minimized within the region between the two vertical dotted lines under the condition that the approximated function and the original function coincide at the left and right endpoints of the approximated function (black circles). b Result for the approximation of f(Δ_LR) in Fig. 3b under acceleration (Acc), deceleration (Dec), and mixed (Mix) conditions. c Mean and standard deviation of l_C among the subjects, where “All” indicates the statistical result from all perturbation conditions. The dots along the bars represent data points (n = 8 for Acc and Dec, n = 6 for Mix, and n = 22 for “All”). d Mean and standard deviation of g_L and g_R among the subjects.