Comprehensive analysis of clustering algorithms: exploring limitations and innovative solutions
- PMID: 39314716
- PMCID: PMC11419652
- DOI: 10.7717/peerj-cs.2286
Comprehensive analysis of clustering algorithms: exploring limitations and innovative solutions
Abstract
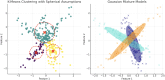
This survey rigorously explores contemporary clustering algorithms within the machine learning paradigm, focusing on five primary methodologies: centroid-based, hierarchical, density-based, distribution-based, and graph-based clustering. Through the lens of recent innovations such as deep embedded clustering and spectral clustering, we analyze the strengths, limitations, and the breadth of application domains-ranging from bioinformatics to social network analysis. Notably, the survey introduces novel contributions by integrating clustering techniques with dimensionality reduction and proposing advanced ensemble methods to enhance stability and accuracy across varied data structures. This work uniquely synthesizes the latest advancements and offers new perspectives on overcoming traditional challenges like scalability and noise sensitivity, thus providing a comprehensive roadmap for future research and practical applications in data-intensive environments.
Keywords: Centroid-based clustering; Clustering algorithms; Clustering challenges and solutions; Density-based clustering; Distribution-based clustering; Hierarchical clustering; Scalability and efficiency; Unsupervised learning.
© 2024 Wani.
Conflict of interest statement
The authors declare that they have no competing interests.
Figures
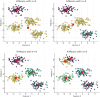
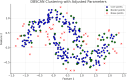
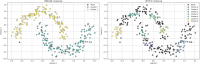
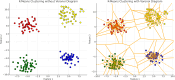
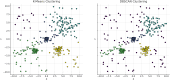
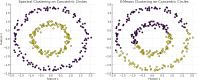
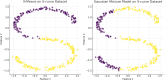
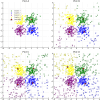
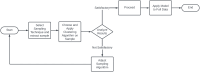
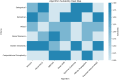
References
-
- Aggarwal CC, Philip SY, Han J, Wang J. A framework for clustering evolving data streams. Proceedings 2003 VLDB Conference; Amsterdam: Elsevier; 2003. pp. 81–92.
-
- Al-mamory SO, Kamil IS. A new density based sampling to enhance dbscan clustering algorithm. Malaysian Journal of Computer Science. 2019;32(4):315–327. doi: 10.22452/mjcs.vol32no4.5. - DOI
-
- Ankerst M, Breunig MM, Kriegel H-P, Sander J. Optics: ordering points to identify the clustering structure. ACM Sigmod Record. 1999;28(2):49–60. doi: 10.1145/304181.304187. - DOI
-
- Arthur D. K-means++: the advantages if careful seeding. Proceeding Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms; 2007. pp. 1027–1035.
-
- Azen R, Walker CM. Categorical data analysis for the behavioral and social sciences. Milton Park: Routledge; 2021.
Publication types
LinkOut - more resources
Full Text Sources
