Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2024 Aug 28;10(17):e36778.
doi: 10.1016/j.heliyon.2024.e36778. eCollection 2024 Sep 15.

Unreliable M [ X]/ G(P 1, P 2)/1 feedback retrial queues with combined working vacation

Bharathy S  1 , Saravanarajan M C  1
Affiliations

Unreliable M [ X]/ G(P 1, P 2)/1 feedback retrial queues with combined working vacation

Bharathy S et al. Heliyon. .

Abstract

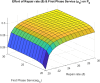
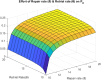
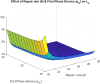
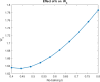
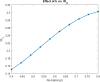
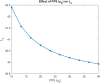
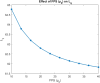
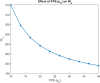
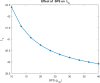
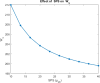
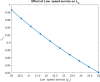
The study examines M [ X ] / G ( P 1 , P 2 ) / 1 feedback retrial queues coupled with starting failure, repair, delay to repair, working vacation, and general retrial times. Also, it explores how different batch sizes affect performance and how bulk arrival affects system behavior. When the server is not in use, a single customer initiates the system while the remaining customers transition to a state of orbit. A new customer must turn on the server to provide two phases of mandatory service at any time. The server could have starting issues. If the service is successfully started (with likelihood α), the customer receives service immediately. In the absence of that, the likelihood of starting failure happens (with likelihood 1 - α = α ¯ ). The server was taken for repair with some delay and that customer was transported to an orbital location. When the server was busy or unavailable, the arriving customers queued by FCFS in the orbit. We also discuss the idea of reworking with probability p, and restarting unsuccessful service attempts to improve customer happiness and service efficiency. We also introduce the concept of working vacation, which permits servers to temporarily stop providing services, affecting system performance and availability at both peak and off-peak times. A supplementary variable technique was adopted for the system's and orbit size's probability-generating function. Various performance measurements were provided with appropriate numerical examples.

Keywords: 35A01; 60K25; 60K30; 65L10; 90B22; Bulk arrival; Feedback; Markov chain; Starting failure; Two phase service; Working vacation.

PubMed Disclaimer

Conflict of interest statement

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: MC Saravanarajan reports was provided by 10.13039/501100004728Vellore Institute of Technology. MC Saravanarajan reports a relationship with Vellore Institute of Technology that includes: employment. MC Saravanarajan has patent pending to no. If there are other authors, they declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Figures

Figure 1
Figure 1
Model's diagrammatic representation.
Figure 2
Figure 2
Model's transition diagram.
Figure 3
Figure 3
Impact of ϑ & μb rate over P0.
Figure 4
Figure 4
Impact of ϑ & θ over P0.
Figure 5
Figure 5
Impact of μb & ϑ over Ls.
Figure 6
Figure 6
Impact of ϑ & θ over Lq.
Figure 7
Figure 7
Impact of μb over P0,Ls,Lq,Wq.
Figure 8
Figure 8
Impact of θ over P0,Ls,Lq,Wq.
Figure 9
Figure 9
Impact of λ` over P0,Ls,Lq,Wq.
Figure 10
Figure 10
Repair rate (ϑ) Vs Ls.
Figure 11
Figure 11
Repair rate (ϑ) Vs Lq.
Figure 12
Figure 12
Repair rate (ϑ) Vs Ws.
Figure 13
Figure 13
Repair rate (ϑ) Vs Wq.
Figure 14
Figure 14
Arrival rate (λ`) Vs Ls.
Figure 15
Figure 15
Arrival rate (λ`) Vs Lq.
Figure 16
Figure 16
Successful start (α) Vs Ls.
Figure 17
Figure 17
Successful start (α) Vs Lq.
Figure 18
Figure 18
Successful start (α) Vs Ws.
Figure 19
Figure 19
Successful start (α) Vs Wq.
Figure 20
Figure 20
Retrial rate (θ) Vs Ls.
Figure 21
Figure 21
Retrial rate (θ) Vs Lq.
Figure 22
Figure 22
Retrial rate (θ) Vs Ws.
Figure 23
Figure 23
Retrial rate (θ) Vs Wq.
Figure 24
Figure 24
No-balking (b) Vs Ls.
Figure 25
Figure 25
No-balking (b) Vs Lq.
Figure 26
Figure 26
No-balking (b) Vs Ws.
Figure 27
Figure 27
No-balking (b) Vs Wq.
Figure 28
Figure 28
FPS (μb) Vs Ls.
Figure 29
Figure 29
FPS (μb) Vs Lq.
Figure 30
Figure 30
FPS (μb) Vs Ws.
Figure 31
Figure 31
FPS (μb) Vs Wq.
Figure 32
Figure 32
SPS (μsb) Vs Ls.
Figure 33
Figure 33
SPS (μsb) Vs Lq.
Figure 34
Figure 34
SPS (μsb) Vs Ws.
Figure 35
Figure 35
SPS (μsb) Vs Wq.
Figure 36
Figure 36
Low speed service (μv) Vs Ls.
Figure 37
Figure 37
Low speed service (μv) Vs Ws.
Figure 38
Figure 38
Delay (η) Vs Ls.
Figure 39
Figure 39
Delay (η) Vs Lq.
Figure 40
Figure 40
Delay (η) Vs Ws.
Figure 41
Figure 41
Delay (η) Vs Wq.
Figure 42
Figure 42
Starting failure (α¯) Vs Ls.
Figure 43
Figure 43
Starting failure (α¯) Vs Lq.
Figure 44
Figure 44
Starting failure (α¯) Vs Ws.
Figure 45
Figure 45
Starting failure (α¯) Vs Wq.
Figure 46
Figure 46
Feedback (p) Vs Ls.
Figure 47
Figure 47
Feedback (p) Vs Lq.
See this image and copyright information in PMC

References

    1. Falin G., Templeton J.G. CRC Press; 1997. Retrial Queues, vol. 75.
    1. Artalejo J.R., Gómez-Corral A. Retrial queueing systems. Math. Comput. Model. 1999;30:3–4. doi: 10.1007/978-3-540-78725-9. - DOI
    1. Falin G. A survey of retrial queues. Queueing Syst. 1990;7:127–167. doi: 10.1007/BF01158472. - DOI
    1. Singh Sadhna, Srivastava R.K. Markovian queuing system for bulk arrival and retrial attempts with multiple vacation policy. IJMTT. 2021;67:21–28. doi: 10.14445/22315373/IJMTT-V67I1P504. - DOI
    1. Jain M., Bhargava Charu. Bulk arrival retrial queue with unreliable server and priority subscribers. Int. J. Oper. Res. 2008;5:242–259.

LinkOut - more resources