Identifying genetic variants that influence the abundance of cell states in single-cell data
- PMID: 39327486
- PMCID: PMC12140807
- DOI: 10.1038/s41588-024-01909-1
Identifying genetic variants that influence the abundance of cell states in single-cell data
Abstract
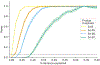
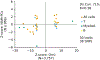
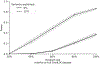
Disease risk alleles influence the composition of cells present in the body, but modeling genetic effects on the cell states revealed by single-cell profiling is difficult because variant-associated states may reflect diverse combinations of the profiled cell features that are challenging to predefine. We introduce Genotype-Neighborhood Associations (GeNA), a statistical tool to identify cell-state abundance quantitative trait loci (csaQTLs) in high-dimensional single-cell datasets. Instead of testing associations to predefined cell states, GeNA flexibly identifies the cell states whose abundance is most associated with genetic variants. In a genome-wide survey of single-cell RNA sequencing peripheral blood profiling from 969 individuals, GeNA identifies five independent loci associated with shifts in the relative abundance of immune cell states. For example, rs3003-T (P = 1.96 × 10-11) associates with increased abundance of natural killer cells expressing tumor necrosis factor response programs. This csaQTL colocalizes with increased risk for psoriasis, an autoimmune disease that responds to anti-tumor necrosis factor treatments. Flexibly characterizing csaQTLs for granular cell states may help illuminate how genetic background alters cellular composition to confer disease risk.
© 2024. The Author(s), under exclusive licence to Springer Nature America, Inc.
Figures
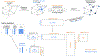






Update of
-
Identifying genetic variants that influence the abundance of cell states in single-cell data.bioRxiv [Preprint]. 2023 Nov 15:2023.11.13.566919. doi: 10.1101/2023.11.13.566919. bioRxiv. 2023. Update in: Nat Genet. 2024 Oct;56(10):2068-2077. doi: 10.1038/s41588-024-01909-1. PMID: 38014313 Free PMC article. Updated. Preprint. No abstract available.
References
-
- Yazar S. et al. Single-cell eQTL mapping identifies cell type-specific genetic control of autoimmune disease. Science 376, eabf3041 (2022). - PubMed
MeSH terms
Grants and funding
- P01 AI148102/AI/NIAID NIH HHS/United States
- U01HG012009/U.S. Department of Health & Human Services | NIH | National Human Genome Research Institute (NHGRI)
- T32HG002295/U.S. Department of Health & Human Services | NIH | National Institute of General Medical Sciences (NIGMS)
- R01AR063759/U.S. Department of Health & Human Services | NIH | National Institute of Arthritis and Musculoskeletal and Skin Diseases (NIAMS)
- UC2AR081023/U.S. Department of Health & Human Services | NIH | National Institute of Arthritis and Musculoskeletal and Skin Diseases (NIAMS)
- R01 AR063759/AR/NIAMS NIH HHS/United States
- T32HG01046/U.S. Department of Health & Human Services | NIH | National Human Genome Research Institute (NHGRI)
- F30AI157385/U.S. Department of Health & Human Services | NIH | National Institute of Allergy and Infectious Diseases (NIAID)
- 1175781/Department of Health | National Health and Medical Research Council (NHMRC)
- U01 HG012009/HG/NHGRI NIH HHS/United States
- F30 AI172238/AI/NIAID NIH HHS/United States
- F30 AI157385/AI/NIAID NIH HHS/United States
- R56 HG013083/HG/NHGRI NIH HHS/United States
- UC2 AR081023/AR/NIAMS NIH HHS/United States
- T32 HG002295/HG/NHGRI NIH HHS/United States
- P01AI148102/U.S. Department of Health & Human Services | NIH | National Institute of Allergy and Infectious Diseases (NIAID)
- R56HG013083/U.S. Department of Health & Human Services | NIH | National Human Genome Research Institute (NHGRI)
- T32 GM144273/GM/NIGMS NIH HHS/United States
- F30AI172238/U.S. Department of Health & Human Services | NIH | National Institute of Allergy and Infectious Diseases (NIAID)
- 2018432/Department of Health | National Health and Medical Research Council (NHMRC)
- T32GM144273/U.S. Department of Health & Human Services | NIH | National Institute of General Medical Sciences (NIGMS)
LinkOut - more resources
Full Text Sources

