Multi-Strategy Improved Harris Hawk Optimization Algorithm and Its Application in Path Planning
- PMID: 39329574
- PMCID: PMC11430035
- DOI: 10.3390/biomimetics9090552
Multi-Strategy Improved Harris Hawk Optimization Algorithm and Its Application in Path Planning
Abstract
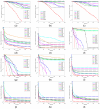
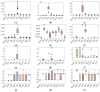
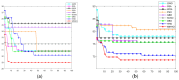
Path planning is a key problem in the autonomous navigation of mobile robots and a research hotspot in the field of robotics. Harris Hawk Optimization (HHO) faces challenges such as low solution accuracy and a slow convergence speed, and it easy falls into local optimization in path planning applications. For this reason, this paper proposes a Multi-strategy Improved Harris Hawk Optimization (MIHHO) algorithm. First, the double adaptive weight strategy is used to enhance the search capability of the algorithm to significantly improve the convergence accuracy and speed of path planning; second, the Dimension Learning-based Hunting (DLH) search strategy is introduced to effectively balance exploration and exploitation while maintaining the diversity of the population; and then, Position update strategy based on Dung Beetle Optimizer algorithm is proposed to reduce the algorithm's possibility of falling into local optimal solutions during path planning. The experimental results of the comparison of the test functions show that the MIHHO algorithm is ranked first in terms of performance, with significant improvements in optimization seeking ability, convergence speed, and stability. Finally, MIHHO is applied to robot path planning, and the test results show that in four environments with different complexities and scales, the average path lengths of MIHHO are improved by 1.99%, 14.45%, 4.52%, and 9.19% compared to HHO, respectively. These results indicate that MIHHO has significant performance advantages in path planning tasks and helps to improve the path planning efficiency and accuracy of mobile robots.
Keywords: Dimension Learning-Based Hunting search strategy; Dung Beetle Optimizer algorithm; Harris Hawk Optimization algorithm; double adaptive weight strategy; path planning.
Conflict of interest statement
The authors declare no conflicts of interest.
Figures











Similar articles
-
Research on Mobile Robot Path Planning Based on MSIAR-GWO Algorithm.Sensors (Basel). 2025 Feb 1;25(3):892. doi: 10.3390/s25030892. Sensors (Basel). 2025. PMID: 39943531 Free PMC article.
-
A path planning method using modified harris hawks optimization algorithm for mobile robots.PeerJ Comput Sci. 2023 Jul 18;9:e1473. doi: 10.7717/peerj-cs.1473. eCollection 2023. PeerJ Comput Sci. 2023. PMID: 37547398 Free PMC article.
-
An enhanced dung beetle optimizer with multiple strategies for robot path planning.Sci Rep. 2025 Feb 7;15(1):4655. doi: 10.1038/s41598-025-88347-z. Sci Rep. 2025. PMID: 39920199 Free PMC article.
-
Path Planning Trends for Autonomous Mobile Robot Navigation: A Review.Sensors (Basel). 2025 Feb 16;25(4):1206. doi: 10.3390/s25041206. Sensors (Basel). 2025. PMID: 40006435 Free PMC article. Review.
-
Agricultural machinery automatic navigation technology.iScience. 2023 Dec 14;27(2):108714. doi: 10.1016/j.isci.2023.108714. eCollection 2024 Feb 16. iScience. 2023. PMID: 38292432 Free PMC article. Review.
Cited by
-
UAV Path Planning: A Dual-Population Cooperative Honey Badger Algorithm for Staged Fusion of Multiple Differential Evolutionary Strategies.Biomimetics (Basel). 2025 Mar 10;10(3):168. doi: 10.3390/biomimetics10030168. Biomimetics (Basel). 2025. PMID: 40136822 Free PMC article.
References
-
- Deng X., Li R., Zhao L., Wang K., Gui X. Multi-obstacle path planning and optimization for mobile robot. Expert Syst. Appl. 2021;183:115445. doi: 10.1016/j.eswa.2021.115445. - DOI
-
- Alshammrei S., Boubaker S., Kolsi L. Improved Dijkstra algorithm for mobile robot path planning and obstacle avoidance. Comput. Mater. Contin. 2022;72:5939–5954. doi: 10.32604/cmc.2022.028165. - DOI
-
- Li X., Yu S., Gao X.Z., Yan Y., Zhao Y. Path planning and obstacle avoidance control of UUV based on an enhanced A* algorithm and MPC in dynamic environment. Ocean Eng. 2024;302:117584. doi: 10.1016/j.oceaneng.2024.117584. - DOI
-
- Gu X., Liu L., Wang L., Yu Z., Guo Y. Energy-optimal adaptive artificial potential field method for path planning of free-flying space robots. J. Frankl. Inst. 2024;361:978–993. doi: 10.1016/j.jfranklin.2023.12.039. - DOI
-
- Kar A.K. Bio inspired computing–a review of algorithms and scope of applications. Expert Syst. Appl. 2016;59:20–32. doi: 10.1016/j.eswa.2016.04.018. - DOI
Grants and funding
LinkOut - more resources
Full Text Sources

