The Many Roles of Precision in Action

Abstract

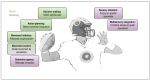
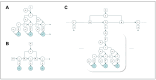
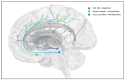
Active inference describes (Bayes-optimal) behaviour as being motivated by the minimisation of surprise of one's sensory observations, through the optimisation of a generative model (of the hidden causes of one's sensory data) in the brain. One of active inference's key appeals is its conceptualisation of precision as biasing neuronal communication and, thus, inference within generative models. The importance of precision in perceptual inference is evident-many studies have demonstrated the importance of ensuring precision estimates are correct for normal (healthy) sensation and perception. Here, we highlight the many roles precision plays in action, i.e., the key processes that rely on adequate estimates of precision, from decision making and action planning to the initiation and control of muscle movement itself. Thereby, we focus on the recent development of hierarchical, "mixed" models-generative models spanning multiple levels of discrete and continuous inference. These kinds of models open up new perspectives on the unified description of hierarchical computation, and its implementation, in action. Here, we highlight how these models reflect the many roles of precision in action-from planning to execution-and the associated pathologies if precision estimation goes wrong. We also discuss the potential biological implementation of the associated message passing, focusing on the role of neuromodulatory systems in mediating different kinds of precision.

Keywords: action; active inference; motor control; precision; predictive coding.

Figure 1

Some processes of an action where precision estimates are essential: A toy example shows a quarterback passing the football to a specific teammate indicating several important components of (active) inference that rely on adequate estimates of precision. The underlying computations cover processes ranging from decision making (e.g., Which play do I select? Where should I run to in order to be able to pass optimally?) to overt movement (contractions of the appropriate arm muscles throughout the throwing movement) and many more that are not shown, including motivational factors and habits, action understanding, joint action, and communication. Precision plays a key role in all of these processes, but a somewhat different one depending on the exact nature of inference. For instance, at “higher” cognitive levels, the player must decide which of several pre-studied plays he initiates. Here, one can describe precision as the confidence in the selected (optimal) sequence of actions. At “lower”, e.g., sensorimotor levels, precision can be described as a multiplicative gain on sensory signals. This can mean implementing sensory attention when selectively focusing on one particular teammate, and a similar bias in determining the weights of sensory cues during multisensory integration. Multisensory integration is essential to guide action, e.g., integrating visual and proprioceptive body position information to guide movement, or integrating seen and heard information about a teammates’ location. Not least, this notion of precision is key to how muscle movement is produced and controlled along the active inference framework: sensory attenuation is a prerequisite for the enaction of motor predictions and a potential clue for determining agency and self–other distinction. Note that some of the illustrated processes can be cast as based on discrete or even categorical inference (such as deciding on one among several plays), whereas others require inference in continuous time to track continuous trajectories of sensory data coming from the world (such as guiding a movement or attending to data from a particular sensory channel). Active inference offers a framework to model action through the combination of discrete and continuous state space models, thus capturing the interplay between the illustrated cognitive vs. sensorimotor processes, and the different roles of precision therein.

Figure 2

Continuous, discrete, and mixed models for (active) inference. (A): Inference in continuous time via a continuous state space model in terms of generalised coordinates of motion. This kind of model generates data (i.e., trajectories) in continuous time, using generalised coordinates of motion (speed, acceleration, jerk, etc.) to represent the trajectory. The details of this model are explained in [32]. The key point here is that a continuous trajectory of sensory observations o (o′, o″,…, corresponding to speed, acceleration, etc.) is modelled as caused by a hidden state x and its derivatives (x′, x″,…, where the interactions between the temporal derivatives are determined by an equation of motion f prescribed by a hidden cause v) through a nonlinear mapping g, plus random fluctuations ω. This elegantly captures the fact that the world generates sensory inputs continually, and, furthermore, that we act upon the world through continuous muscle movements. For this reason, these formulations are typically used to model sensation and movement, for instance, based on prediction error minimisation in predictive coding schemes. (B): Inference in a discrete state space formulation. The key difference to the model shown in (A) is that we are seeing a sequence of three distinct hidden states s₁–s₃, which each generate corresponding an observable outcome o₁–o₃ through a matrix (A specifying the likelihood mapping). The states are linked by transition matrices B, which, in turn, depend on the current policy (sequence of actions encoded by π; G represents the probability distribution over policies based on expected free energy; D represents the initial state; see [32]). In contrast to the trajectory generated by the model in (A), this model generates data in discrete steps. These formulations lend themselves to model discrete or even categorical inference of the sort that, presumably, guides decision making or action planning. (C): “Mixed” model of action comprising a discrete state space level sitting “on top” of, and linked to, a continuous state space level, each displayed as a Bayesian network. The upper discrete level generates “chunks” of data in discrete time (the Bayesian network represents conditional dependencies) and, thus, models categorical decisions or discrete action plans; the lower continuous level generates data in continuous time (the Bayesian network represents generalised coordinates of motion). The link between the levels happens as the outcomes of the discrete model determine a hidden cause that prescribes the generalised motion of continuous hidden states, generating continuous sensation. Here, the upper level could select an optimal action sequence (such as a particular throwing movement), which allows the generation of muscle movements through proprioceptive predictions via the lower level (thus, actually throwing the football). Precision estimates play an important, but different, role in several computations at both levels of this model (see Figure 1 and main text). Adapted from [32], Figures 1, 5 and 8 under the CC-BY 4.0 licence.

Figure 3

Using hierarchical active inference to simulate action and its pathologies. (A): Mapping inferential message passing onto the known anatomy of movement. Here, to simulate pointing movements to three visual targets, we used a hierarchical mixed model with two linked discrete levels, inferring pointing sequences and intermediate attracting points for movement, respectively; the lower level linked to a continuous level, as in Figure 2. The top schematic (small A) shows the mapping of two discrete levels of the mixed model, concerned with target and action selection, onto frontoparietal cortices and structures of the basal ganglia. The bottom schematic (small B) shows the relationship between the lower discrete level and the continuous level of the model, which ultimately issues proprioceptive predictions that are enacted by movement through spinal reflexes in continuous time. For details, see [100]. (B): This architecture was used to simulate pointing movements to three visual targets under different synthetic lesions. The black lines in the left plots show the trajectory of the simulated arm; the red spheres represent the sequence of attracting points selected by the (lower) discrete model that determine short trajectories for the continuous model (reminiscent of the concept of motor “chunking”). The right plots show the corresponding changes in shoulder rotation and flexion, and elbow flexion. From top to bottom: Overestimation of sensory precision did not impair movement, but exaggerated tendon reflexes (not shown). Reducing the precision of the beliefs about action policy selection produced “akinetic”, small-amplitude movements. The overestimation of the anticipated smoothness of sensory fluctuations over time produced hypermetric overshoots at the end of each movement. Finally, reducing the precision associated with linking the discrete model levels concerned with target and action policy selection, respectively, produced an apparent confusion whenever the target position changed. Reprinted from (Figures 5 and 6 in [100]), under the CC-BY 4.0 licence.

Figure 4

Neuromodulatory systems associated with precision in action. The cholinergic, dopaminergic, and noradrenergic pathways have been linked to mediating different kinds of precision or uncertainty. Within the active inference framework, these neuromodulators can be linked to the precision afforded to sensory signals, action policies and control, and model predictions (about the dynamics of changes in the environment), respectively. Figure reprinted from (Figure 4 in [110]), under the CC-BY 4.0 licence. VTA = ventral tegmental area, SNc = substantia nigra pars compacta.