Theory and Measurement of Heat Transport in Solids: How Rigidity and Spectral Properties Govern Behavior

Abstract

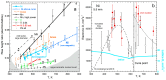
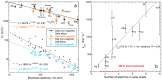
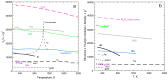
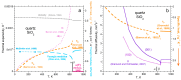
Models of heat transport in solids, being based on idealized elastic collisions of gas molecules, are flawed because heat and mass diffuse independently in solids but together in gas. To better understand heat transfer, an analytical, theoretical approach is combined with data from laser flash analysis, which is the most accurate method available. Dimensional analysis of Fourier's heat equation shows that thermal diffusivity (D) depends on length-scale, which has been confirmed experimentally for metallic, semiconducting, and electrically insulating solids. A radiative diffusion model reproduces measured thermal conductivity (K = Dρc_P = D × density × specific heat) for thick solids from ~0 to >1200 K using idealized spectra represented by 2-4 parameters. Heat diffusion at laboratory temperatures (conduction) proceeds by absorption and re-emission of infrared light, which explains why heat flows into, through, and out of a material. Because heat added to matter performs work, thermal expansivity is proportional to ρc_P/Young's modulus (i.e., rigidity or strength), which is confirmed experimentally over wide temperature ranges. Greater uptake of applied heat (e.g., c_P generally increasing with T or at certain phase transitions) reduces the amount of heat that can flow through the solid, but because K = Dρc_P, the rate (D) must decrease to compensate. Laser flash analysis data confirm this proposal. Transport properties thus depend on heat uptake, which is controlled by the interaction of light with the material under the conditions of interest. This new finding supports a radiative diffusion mechanism for heat transport and explains behavior from ~0 K to above melting.

Keywords: Young’s modulus; absolute methods; diffusion; dimensional analysis; heat; length-scale physics; mechanisms; pressure–volume work; radiative transfer; thermal expansivity.

Figure 1

Essentials of laser flash analysis: (a) Schematic of the experimental configuration. Dashed box indicates the furnace enclosing the sample. Marble rectangle depicts the cross-section of the sample with thickness L (double arrow), which is coated with graphite (grey layers). Arrows indicate the arrival of laser energy and departure of emissions. Blue dotted arrow shows fast ballistic transfer. Squiggle arrows indicate slow diffusive travel of heat across the sample. (b) Examples of raw data (time–temperature curves) for a partially transparent electrical insulator. Ballistic transfer (black double arrow) increases strongly with temperature. (c) Raw data for an opaque metal (pure electrolytic iron). Circle indicates the half-time for the main (slow) mechanism at low T. After the initial (fast) rise, the signal decreases due to the warmed top surface cooling to the surroundings, and then increases again as the majority of heat applied is slowly transferred across the sample (indicated by the double arrow). Inset shows an expanded view of the rapid rise at low T. Panel (b) from Xu and Hofmeister [25], Figure 1b, with permissions.

Figure 7

Fits of our 2-parameter radiative transfer model to thermal conductivity data: (a) Electrically insulating Al₂O₃, represented by a simple boxcar spectrum. Squares = measured K on ceramic corundum [64]. Dot-dashed line = K obtained from LFA data on sapphire and ceramic Al₂O₃ [61], using c_P from [65] and ρ from [66]. (b) Semiconducting graphite represented by a triangular ramp spectrum. Plus sign = measured K from [62]. Low-T data on C_P for pyrolytic graphite [67]. Dot-dashed and blue lines = K obtained from LFA data, using high T density and specific heat from [63]. Modified from Figure 11.5a,b in the work of Hofmeister [8], with permissions.

Figure 9

Correlation of fitting coefficients F and g obtained using Equation (21): (a) Metals from [20]; the remaining 173 samples from [8]. Fits for anisotropic substances were made to each orientation. Exponential fits are shown. Porous samples (e.g., brucite, Mg(OH)₂,) fall below the curves. Salts lie slightly below the curve for the silicates, which have ionic-covalent bonding. (b) Comparison of grainy mixtures to crystals. Black diamonds and dashed line = 35 LFA measurements on polycrystalline minerals and rocks compiled by [8]. Square with cross and dotted curve = carbonate minerals and rocks [70]. Grey dots and thick curve = LFA data on oxide and silicate minerals, excluding micas with flow across layers. Part (b) was modified from Figure 1 in the work of Merriman et al. [32], with permissions.

Figure 13

Comparison of transport properties to specific heat on logarithmic axes (with the c_P axis reversed, per Equation (15)), as indicated by the orange arrow: (a) Corundum. Dotted line = high-T D from Hofmeister [61] extrapolated to low T (pink), which is consistent with LFA data on sapphire crystals (blue diamonds from Burghartz and Schulz [93]). The latter study reported a fit to the data, which were scattered. Values of K are low due to contact losses; the grey dashed curve suggests intrinsic K values. Specific heat (orange curve from Ditmars et al. [65]) increases over all T (reversed axis) but is not as complex as the decrease in D with T. (b) Metallic iron in the low-T bcc phase. Grey curve shows the highest K from [2] to represent the purest sample. D calculated using c_P (orange curve from Desai [79]) and density (see Figure 10) is consistent with the Fe standard used in LFA cross-checks, see Henderson et al. [94].

Figure A1

Schematic of dynamic, inelastic interactions of finite-size atoms in a monatomic gas. Left to right shows the progression of an inelastic collision with time. Black = nuclei. Grey = shells of electrons, forming a shielding cloud. Squiggle arrow = thermal photon. (a) Head-on approach of two spherical atoms with different speeds. (b) Collision, where a reduction in distance along the one direction increases the Coulombic repulsion and breaks the spherical symmetry, which changes the energy of the atom. The energy needed to deform the atom is obtained from the kinetic energy reservoir. (c) Departure, where the atoms back-transform to a spherical shape with lower energy. (d) After the interaction ceases, the atoms must shed the energy difference between the excited and original states as heat: Consequently, the total energy of translation is reduced. Adapted from the work of Hofmeister [8] (Figure 5.2 therein), with permissions.

Figure 2

Schematics: (a) Longitudinal flow in Cartesian symmetry. At steady state, flux ℑ along the special direction is a constant that is independent of position, so the axial thermal gradient is independent of time, and perpendicular slices are isothermal. (b) Initial conditions for heat flow along two parallel bars with different areas (a) and properties (D, C, K), to which an instantaneous pulse was applied (yellow area). (c) Initial conditions for a blended bar, created from superimposing two bars of equal area.

Figure 3

Dependence of D at 298 K on thickness. Least squares fits are to D(L, 298 K) = D_∞[1 − exp(−bL)], where the fits have b values that roughly inversely correlate with D_∞, representing very large samples: (a) Insulators. Symbolts as labelel. Note the rapid drop in D for the thinnest MgO samples (squares), which fall on the trend for single-crystal corundum (dots). (b) Graphite, metals, and 3 alloys, where a 0.01 ms pulse was used for L < 1 mm. Part (a) modified from Figure 7.9 in Hofmeister [8], with permissions. Part (b) combines previous results from [26,53] with 5 additional samples; see Appendix C.

Figure 4

Comparisons of electronic tolattice heat transport in metals: (a) Temperature dependence of the ratio of the rapid to the slow rise heights for an assortment of non-magnetic metals, plus nickel below the Curie point. Least squares fits were not forced through the origin. (b) Results for Ni acquired in many different runs. Filled squares = short data collection times. Open squares = truncated, long collection times. Above T_Curie, a power-law fit best describes the data. Part (a) was reproduced from Figure 11b, whereas part (b) was from Figure 13c, both from the work of Criss and Hofmeister [4], which has a Creative Commons 4 license.

Figure 5

Dependence of metallic heat transport properties on physical properties: (a) Plot of D vs. electrical resisitivity. Measurements of D_ele are at 473 K. For D_lat, our data and direct measurements compiled by Touloukian et al. [54] are used, which are uncertain by ~2 and ~5%, respectively. (b) Relationship of k_ele with the number of loosely bound electrons. Ti and Ta were shifted slightly to the right for clarity. Part (a) is from Figure 17, and part (b) is from Figure 20b, both inform the work of Criss and Hofmeister [4], which has a Creative Commons 4 license.

Figure 6

Comparison of thermal diffusivity calculated from XRD mineral proportions to LFA measurements on non-porous silicates: (a) Data on individual disks. Disks with special attributes are labeled. Sections with oriented minerals were plotted using the appropriate formula for the orientation. (b) Comparison of the average D calculated for series and parallel heat flow to D data on isotropic sections. Squares = silicates. Dots = averages for 6 rocks for which 4 to 6 disks were measured. Modified from Figures 12b and 14 in the work of Merriman et al. [32], with permissions.

Figure 8

Fits to pure iron, tungsten, and two alloys using a radiative diffusion model that sums Equations (19) and (20). The four parameters are tabulated. Data are in colors; fits are in black. Aluminum 1100 (99% Al) data from [68]. Data for >99.1% Fe (below the Curie point), tungsten, and non-magnetic steel from [2]. Modified from Figure 11.5a,b in the work of Hofmeister [8], with permissions.

Figure 10

Comparison of thermal expansivity to specific heat: (a) Al₂O₃. Circle = α from powder XRD compiled by Reeber and Wang [76]; + = α compiled by White and Roberts [77]. Pink squares = single-crystal interferometry and twin telemicroscope measurements of Hahn [78]. Orange curve = c_P compiled by Ditmars et al. [65]. Grey = density calculated from α. (b) Fe metal. Thick vertical bars mark structural phase transitions. Orange curve = c_P compiled by Desai [79]; × = capacitance measurements of α-Fe by White [80]. Squares = dilatometry by Kozlovskii and Stankus [81]. Diamonds = gamma-ray attenuation by Abdullaev et al. [82]. Grey = density calculated from α. Part (a) was modified from Figure A1a in the work of Hofmeister et al. [28], which has a Creative Commons license.

Figure 11

Dependence of α/c_P on ρ/(ΞN/Z). Data on elements compiled in [28]. For the insulators, tables from [83] were used, omitting Co₂SiO₄ because α was estimated. Fits are least squares: (a) Insulators and cubic fcc metals. Lead strongly influences the power-law fit. Orthorhombic Fe₂SiO₄ has a shearing transition, whereas α for orthorhombic Mn₂SiO₄ is unconfirmed. (b) Cubic bcc and hexagonal hcp metals. Outliers Li and Be have very small cations and few valance electrons. Both parts reproduced from Figure 14 in the work of Hofmeister et al. [28], which has a Creative Commons license.

Figure 12

Evaluation of Equation (14) at high T for well-studied solids: (a) Dependence of c_P/α on temperature. See [28] for data sources. Discontinuities in Ta α result from variations between studies. (b) Dependence of Ξ/ρ with the structural factor on T. Constant ambient ρ was used, since Young’s modulus is uncertain. Data on Ξ from [84,85,86,87,88,89,90]. For Au, Fe, MgO, NaCl, and KCl, we used T derivatives near and above 298 K for B and G from [91] to compute dΞ/dT.

Figure 14

Comparison of transport properties to static properties for metallic iron at high T. Axes are linear: (a) Specific heat (orange, from [79], which is lower for fcc due to its high density. Black dots show D for the Fe standard used in LFA cross-checks from Henderson et al. [94]. Open squares are new data on electrolytic iron coated with Al₂O₃ to avoid reaction at high T. Blue lines and symbols are LFA data collected with a zirconium coating Monaghan and Quested [95]. Pink dots are plane-wave data from Gorbatov et al. [96], which is a periodic technique; minor contact losses explain the lower values. Dotted line = the best representation of these studies, combined. Grey = K calculated from the best estimate. (b) Thermal expansivity (pink solid line is dilatometry Kozlovskii and Stankus [81]; dot-dashed line is the gamma attenuation Abdullaev et al. [82]).

Figure 15

Properties of low- and high-quartz polymorphs: (a) Static properties. Data sources are labeled; see McSkimin et al., Barron et al., Grønvold et al., Kihara, and Ohno et al. [97,98,99,100,101]. (b) Comparison of thermal diffusivity for nearly pure and anhydrous natural quartz (sample HQ from Branlund and Hofmeister [55]) to specific heat (reversed axis) for a bulk quartz sample from Barron et al. [98] and Grønvold et al. [99].

Figure 16

Physical properties of glasses and melts made by remelting natural lavas with high silica contents: (a) Thermal diffusivity. Silica content is labeled. Pink and purple dots are two slightly different glasses from [104]. (b) Specific heat from powders of the identical glasses. The alumina content is labeled. Samples have <5 wt% each of oxides of Fe, Ca, Mg, Na, and K. Modified from the work of Hofmeister et al. [102], Figures 3a and 4a therein, with permissions.

Figure 17

Physical properties of glasses and melts made by remelting natural lavas with intermediate silica contents: (a) Thermal diffusivity. Silica content is labeled. Blue dots are a synthetic andesite with trace fluorine. (b) Specific heat from powders of the identical glasses, except for the andesites. Alumina content is labeled. Samples have <10 wt% each of oxides of Fe, Ca, and Mg, and <5 wt% oxides of Na and K. Modified from the work of Hofmeister et al. [102], Figures 3b and 4b therein, with permission.