Quantum refinement in real and reciprocal space using the Phenix and ORCA software

Abstract

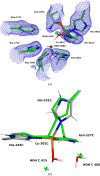
X-ray and neutron crystallography, as well as cryogenic electron microscopy (cryo-EM), are the most common methods to obtain atomic structures of biological macromolecules. A feature they all have in common is that, at typical resolutions, the experimental data need to be supplemented by empirical restraints, ensuring that the final structure is chemically reasonable. The restraints are accurate for amino acids and nucleic acids, but often less accurate for substrates, inhibitors, small-molecule ligands and metal sites, for which experimental data are scarce or empirical potentials are harder to formulate. This can be solved using quantum mechanical calculations for a small but interesting part of the structure. Such an approach, called quantum refinement, has been shown to improve structures locally, allow the determination of the protonation and oxidation states of ligands and metals, and discriminate between different interpretations of the structure. Here, we present a new implementation of quantum refinement interfacing the widely used structure-refinement software Phenix and the freely available quantum mechanical software ORCA. Through application to manganese superoxide dismutase and V- and Fe-nitrogenase, we show that the approach works effectively for X-ray and neutron crystal structures, that old results can be reproduced and structural discrimination can be performed. We discuss how the weight factor between the experimental data and the empirical restraints should be selected and how quantum mechanical quality measures such as strain energies should be calculated. We also present an application of quantum refinement to cryo-EM data for particulate methane monooxygenase and show that this may be the method of choice for metal sites in such structures because no accurate empirical restraints are currently available for metals.

Keywords: Fe-nitrogenase; Mn superoxide dismutase; QM/MM; V-nitrogenase; X-ray crystallography; cryo-EM; neutron crystallography; particulate methane monooxygenase; quantum refinement.

Figure 1

Flow scheme illustrating the QRef procedure.

Figure 2

The active sites of the studied systems, showing the QM regions employed: (a) MnSOD, (b) V-nitro­genase, (c) Fe-nitro­genase and (d) pMMO.

Figure 3

Dependence of (a) the RSZD scores (left axis) and the strain energy (right axis, dotted line), as well as (b) the bond lengths to Mn (left axis, full lines), distances involving the hydrogen bond between the solvent ligand and Gln143 (left axis and dotted lines) and the deviation of these distances from the QM/MM reference structure (Δd; right axis and dashed line) as a function of the w_c factor for the neutron structure of reduced MnSOD (7kkw).

Figure 4

The four protonation states of homocitrate considered: 2H, 1Ha, 1Hc and 0H. Atom numbers are also shown. Non-polar H atoms have been omitted. The charges of homocitrate are −2, −3, −3 and −4, respectively, in these four protonation states.

Figure 5

(a) Comparison of the deposited (green) and the quantum-refined (atomic colours; largest QM system with w_x = 3) structures of the Cu_D site in pMMO, together with the 2mF_o − DF_c map at 0.7σ. (b) Another projection emphasizing the change in the Cu—N distance to His245C.