This is a preprint.
Anisotropy of object nonrigidity: High-level perceptual consequences of cortical anisotropy
- PMID: 39345500
- PMCID: PMC11429613
- DOI: 10.1101/2024.09.10.612333
Anisotropy of object nonrigidity: High-level perceptual consequences of cortical anisotropy
Abstract
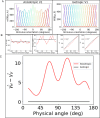
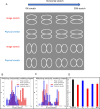
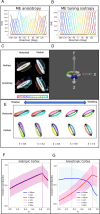
We demonstrate an unexpected anisotropy in perceived object non-rigidity, a higher-level perceptual phenomenon, and explain it by the population distribution of low-level neuronal properties in primary visual cortex. We measured the visual interpretation of two rigidly connected rotating circular rings. In videos where observers predominantly perceived rigidly-connected horizontally rotating rings, they predominantly perceived non-rigid independently wobbling rings if the video was rotated by 90°. Additionally, vertically rotating rings appeared narrower and longer than horizontally rotating counterparts. We decoded these perceived shape changes from V1 outputs incorporating documented cortical anisotropies in orientation selectivity: more cells and narrower tuning for the horizontal orientation than for vertical. Even when shapes were matched, the non-rigidity anisotropy persisted, suggesting uneven distributions of motion-direction mechanisms. When cortical anisotropies were incorporated into optic flow computations, the kinematic gradients (Divergence, Curl, Deformation) for vertical rotations aligned more with derived gradients for physical non-rigidity, while those for horizontal rotations aligned closer to rigidity. Our results reveal how high-level non-rigidity percepts can be shaped by hardwired cortical anisotropies. Cortical anisotropies are claimed to promote efficient encoding of statistical properties of natural images, but their surprising contribution to failures of shape constancy and object rigidity raise questions about their evolutionary function.
Keywords: Object nonrigidity; cortical anisotropy; cortical model; kinematic invariants; motion perception; shape constancy.
Conflict of interest statement
Competing interests: The authors declare no competing interests.
Figures



Similar articles
-
Perceptual transitions between object rigidity and non-rigidity: Competition and cooperation among motion energy, feature tracking, and shape-based priors.J Vis. 2024 Feb 1;24(2):3. doi: 10.1167/jov.24.2.3. J Vis. 2024. PMID: 38306112 Free PMC article.
-
Perceptual Transitions between Object Rigidity & Non-rigidity: Competition and cooperation between motion-energy, feature-tracking and shape-based priors.bioRxiv [Preprint]. 2023 Nov 20:2023.04.07.536067. doi: 10.1101/2023.04.07.536067. bioRxiv. 2023. Update in: J Vis. 2024 Feb 1;24(2):3. doi: 10.1167/jov.24.2.3. PMID: 37503257 Free PMC article. Updated. Preprint.
-
The relationship of vertical and horizontal velocity gradients in the perception of shape, rotation, and rigidity.J Exp Psychol Hum Percept Perform. 1998 Aug;24(4):1257-72. doi: 10.1037//0096-1523.24.4.1257. J Exp Psychol Hum Percept Perform. 1998. PMID: 9706715
-
Why do parallel cortical systems exist for the perception of static form and moving form?Percept Psychophys. 1991 Feb;49(2):117-41. doi: 10.3758/bf03205033. Percept Psychophys. 1991. PMID: 2017350 Review.
-
A theory of shape constancy based on perspective invariants.Vision Res. 1994 Jun;34(12):1637-58. doi: 10.1016/0042-6989(94)90123-6. Vision Res. 1994. PMID: 7941373 Review.
References
-
- Tomasi C., & Kanade T. (1992). Shape and motion from image streams under orthography: a factorization method. International Journal of Computer Vision, 9, 137–154.
-
- Aggarwal J. K., Cai Q., Liao W., & Sabata B. (1998). Nonrigid motion analysis: Articulated and elastic motion. Computer Vision and Image Understanding, 70(2), 142–156.
-
- Hildreth E. C. (1984). Computations underlying the measurement of visual motion. Artificial intelligence, 23(3), 309–354.
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
