Quantification in shooting precision for preferred and non-preferred foot in college soccer players using the 95% equal confidence ellipse
- PMID: 39346492
- PMCID: PMC11427314
- DOI: 10.3389/fspor.2024.1434096
Quantification in shooting precision for preferred and non-preferred foot in college soccer players using the 95% equal confidence ellipse
Abstract
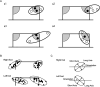
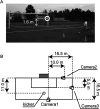
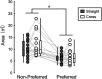
Shooting precision is a fundamental characteristic in soccer, yet the probabilistic structure and magnitude of precision in soccer shooting remain quantitatively unexplored. This study aimed to quantify shooting precision using measures derived from the bivariate normal distribution for both preferred and non-preferred feet. Sixteen right-footed collegiate soccer players participated by performing instep kicks aiming at targets which are placed close to the left and right top corners of the soccer goal. We used bivariate normal distribution modeled the ball positions, revealing an ellipsoidal distribution, and the area of the 95% confidence ellipses served as an index of precision. Repeated measures ANOVAs revealed a significant main effect of the kicking foot. For shots aimed at the same side as the kicking foot, the area of the 95% confidence ellipse was 6.17 ± 1.93 m2 (mean ± SD) for the preferred foot and 10.22 ± 3.53 m2 for the non-preferred foot. Similar results were observed for shots aimed at the opposite side of the kicking foot. These quantitative findings hold promise for advancing soccer research and enhancing practical applications in soccer skill assessment.
Keywords: accuracy; bivariate normal distribution; football; kick; motor control; variability.
© 2024 Shimotashiro and Shinya.
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures



References
-
- Reilly T, Korkusuz F. The biomechanics of football. In: Science and Football II. London: Routledge; (2003). p. 333–40. 10.4324/9780203893685 - DOI
-
- Njororai WWS. Analysis of goals scored in the 2010 world cup soccer tournament held in South Africa. J Phys Ed Sport. (2013) 13(1):6–13. 10.7752/jpes.2013.01002 - DOI
-
- Almeida CH, Volossovitch A, Duarte R. Penalty kick outcomes in UEFA club competitions (2010–2015): the roles of situational, individual and performance factors. Int J Perf Anal Sport. (2016) 16(2):508–22. 10.1080/24748668.2016.11868905 - DOI
LinkOut - more resources
Full Text Sources

