Confidence and second-order errors in cortical circuits

Abstract

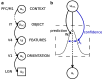
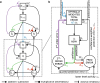
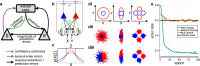
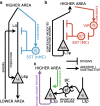
Minimization of cortical prediction errors has been considered a key computational goal of the cerebral cortex underlying perception, action, and learning. However, it is still unclear how the cortex should form and use information about uncertainty in this process. Here, we formally derive neural dynamics that minimize prediction errors under the assumption that cortical areas must not only predict the activity in other areas and sensory streams but also jointly project their confidence (inverse expected uncertainty) in their predictions. In the resulting neuronal dynamics, the integration of bottom-up and top-down cortical streams is dynamically modulated based on confidence in accordance with the Bayesian principle. Moreover, the theory predicts the existence of cortical second-order errors, comparing confidence and actual performance. These errors are propagated through the cortical hierarchy alongside classical prediction errors and are used to learn the weights of synapses responsible for formulating confidence. We propose a detailed mapping of the theory to cortical circuitry, discuss entailed functional interpretations, and provide potential directions for experimental work.

Keywords: cortical computation; energy-based models; predictive coding; uncertainty.

Fig. 1.

Predictive distributions in the cortical hierarchy. a) Probabilistic model. Latent representations (${\mathit{u}}_{\mathit{\ell }}$) are organized in a strict generative hierarchy. b) Predictions are Gaussian distributions. Both the mean (${\mathit{\mu }}_{\mathit{\ell }}={\mathit{W}}_{\mathit{\ell }}{\mathit{r}}_{\mathit{\ell }+\mathbf{1}}$, first-order) and the confidence (${\mathit{\pi }}_{\mathit{\ell }}={\mathit{A}}_{\mathit{\ell }}{\mathit{r}}_{\mathit{\ell }+\mathbf{1}}$, inverse variance, second-order) are functions of higher-level activity.

Fig. 2.

Neuronal dynamics of inference. a) A high-level schematic depiction of neuronal dynamics (Eqs. 2 and 3). Prediction errors [${\mathit{e}}_{\mathit{\ell }}$] are first computed by comparing predictions [${\mathit{\mu }}_{\mathit{\ell }}={\mathit{W}}_{\mathit{\ell }}{\mathit{r}}_{\mathit{\ell }+\mathbf{1}}$] with actual activity or data [${\mathit{u}}_{\mathit{\ell }}$]. Prediction errors are weighted multiplicatively by the estimated confidence (inverse expected variance) of the prediction [${\mathit{\pi }}_{\mathit{\ell }}={\mathit{A}}_{\mathit{\ell }}{\mathit{r}}_{\mathit{\ell }+\mathbf{1}}$]. The second-order errors [${\mathit{\delta }}_{\mathit{\ell }}$] are computed by comparing inverse confidence estimates [${\mathit{\pi }}_{\mathit{\ell }}^{-1}$] and squared prediction errors [${\mathit{e}}_{\mathit{\ell }}^2$]. The second-order errors are up-propagated and integrated alongside up-propagated prediction errors into the total error [${\mathit{a}}_{\mathit{\ell }}$]. The total error is divisively modulated by the prior confidence [${\mathit{\pi }}_{\mathit{\ell }}$] b) A more detailed illustration centred on dynamics for representations at a single level ℓ. Prediction errors and second-order errors are then those of level $\ell -1$.

Fig. 3.

Adaptive balancing of cortical streams based on confidence. a) Divisive modulation of errors by the confidence of top-down predictions about what the activity of a neuron should be (prior confidence, ${\mathit{\pi }}_{\mathit{\ell }}^{-1}$). b) Multiplicative modulation of errors by the confidence of predictions that a neuron makes about what the activity of other neurons should be (data confidence, ${\mathit{\pi }}_{\mathit{\ell }-\mathbf{1}}$).

Fig. 4.

Propagation of second-order errors for classification. a) The second-order errors compare confidence and performance (with performance defined as a function of the magnitude of prediction errors). b) A $2\times 2$ network for binary classification. During learning, the $\mathrm{X}$ and $\mathrm{Y}$ data are sampled from one of the two class distributions, and the activity of neurons representing the class is clamped to the one-hot encoded correct class. Parameters ($\mathit{W},\mathit{A}$) are then learned following Eqs. 4 and 5. During inference, the activity of neurons representing the class follows neuronal dynamics (without top-down influence), and we read the selected class as the one corresponding to the most active neuron. Prediction error (first-order) propagation is omitted in the depiction. c) Maximizing the likelihood of predictions leads to nonlinear classification in a single area. di) Two different 2-dimensional binary classification tasks. The ellipse represents the true class distributions for the two classes. dii) Classification with second-order error propagation. diii) Classification without second-order error propagation. e) Classification accuracy on the task presented in d, second column.

Fig. 5.

Cortical circuit for neuronal dynamics of inference (as described in Eq. 2 and Eq. 3). a) Representations (${\mathit{u}}_{\mathit{\ell }}$) are held in the somatic membrane potential of L6p. Top-down synapses carrying predictions (${\mathit{\mu }}_{\mathit{\ell }}={\mathit{W}}_{\mathit{\ell }}{\mathit{r}}_{\mathit{\ell }+\mathbf{1}}$) directly excite L6p at proximal dendrites. Bottom-up confidence-weighted prediction errors (${\mathit{W}}_{\mathit{\ell }-\mathbf{1}}^T({\mathit{\pi }}_{\mathit{\ell }\mathbf{-}\mathbf{1}}\circ {\mathit{e}}_{\mathit{\ell }-\mathbf{1}})$) and second-order errors (${\mathit{A}}_{\mathit{\ell }-\mathbf{1}}^T{\mathit{\delta }}_{\mathit{\ell }-\mathbf{1}}$) are integrated into total error (${\mathit{a}}_{\mathit{\ell }}$) in the distal dendrites of L6p as described in Eq. 3. This total error is then weighted by the prior uncertainty (${\mathit{\pi }}_{\mathit{\ell }}^{-1}$) through divisive dendritic inhibition realized by deep SST-expressing interneurons. b) Top-down predictions (${\mathit{\mu }}_{\mathit{\ell }}={\mathit{W}}_{\mathit{\ell }}{\mathit{r}}_{\mathit{\ell }+\mathbf{1}}$) and local representations (${\mathit{u}}_{\mathit{\ell }}$) are compared in L3e. Confidence weighting is then realized through gain modulation of L3e by the disinhibitory VIP-expressing and SST-expressing interneurons circuit. c) L3δ compares top-down confidence and local squared prediction errors encoded in basket cells (BC) into re-weighted second-order errors.