European pollen reanalysis, 1980-2022, for alder, birch, and olive

Abstract

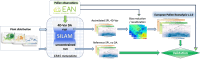
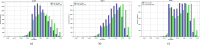
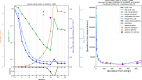
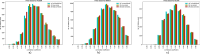
The dataset presents a 43 year-long reanalysis of pollen seasons for three major allergenic genera of trees in Europe: alder (Alnus), birch (Betula), and olive (Olea). Driven by the meteorological reanalysis ERA5, the atmospheric composition model SILAM predicted the flowering period and calculated the Europe-wide dispersion pattern of pollen for the years 1980-2022. The model applied an extended 4-dimensional variational data assimilation of in-situ observations of aerobiological networks in 34 European countries to reproduce the inter-annual variability and trends of pollen production and distribution. The control variable of the assimilation procedure was the total pollen release during each flowering season, implemented as an annual correction factor to the mean pollen production. The dataset was designed as an input to studies on climate-induced and anthropogenically driven changes in the European vegetation, biodiversity monitoring, bioaerosol modelling and assessment, as well as, in combination with intra-seasonal observations, for health-related applications.

Fig. 1

Scheme of the European Pollen Reanalysis.

Fig. 2

Emission distribution maps of (a) alder, (b) birch, and (c) olive (map from 2020) used in the reanalysis. Unit: see colour bars. Each map shows the multi-annual mean release of pollen grains of the corresponding type per 1 m² of the grid cell area.

Fig. 3

The number of stations used for assimilation and validation for each species over the reanalysis period.

Fig. 4

Heat-sum start/end flowering thresholds for alder, birch and olive. No birch trees were assumed south of 40 N.

Fig. 5

Histogram of correlation coefficients for 1-day (blue) and 2-day (green) mean observations and model predictions. All stations satisfying the completeness requirements (>30 days of data in the given year) are included.

Fig. 6

Mean multi-annual SPIn, [pollen day m⁻³]. The Seasonal Pollen Integral for each pollen type is computed as a sum of daily-mean near-surface concentrations, separately for each year. The obtained annual integrals are averaged over the whole period 1980–2022.

Fig. 7

Diagnostics of the DA iterations: error reduction and L-curve-based stopping criterion for alder in 1990. Left-hand panel: changes in the squared deviation from observations (first term in Eq. (1), dark blue line), squared deviation from the background (second term in Eq. (1), brown line), norm of the gradient of the full cost function (1) (green line), squared deviation from the evaluation subset of the observations (light blue line), and cosine of an angle between two sequential iteration steps (black line at the lower panel), all as functions of the 4D-Var iterations (iteration 0 corresponds to the background state). The lower panel also shows the iterations used for fitting the analytical approximation of the L-curve (green dots at the bottom) – and those excluded from the fitting due to suspected instability of the optimiser. Right-hand panel: L-curve, a dependence of the squared model deviation from the assimilated observations on the deviation of the control variable from the background (the first and the second terms of the Eq. (1), respectively): magenta broken line is plotted iteration-wise, light blue curve is its smooth analytical approximation with a hyperbolic function. In both panels, the red star shows the stopping criterion determined from the analytical L-curve approximation as 5% threshold of the initial slope; the nearest iteration is then considered as the optimal one. The orange cross denotes the first estimate made during the calculations with a simplified approximation procedure, whereas the violet diamond shows the first iteration when the full cost function reaches a 1.1 level of its overall minimum during the optimization.

Fig. 8

Summary of L-curve diagnostics for the whole reanalysis. X-axis: RMSE for assimilated stations of the optimal 4D-VAR iteration normalised with that of the 0^th iteration (unconstrained run), y-axis: RMSE for evaluation stations at the optimal iteration normalised with that of the 0^th iteration. On both axes, 1.0 means no improvement due to the data assimilation. Points above the 1:1 line show the years where improvement was higher for assimilated stations than for evaluation ones: large displacement shows an overfit. Two side dashed lines show the slope of 0.5 and 2 with an offset of −0.1 and 0.1, respectively. The size of the dots is the smallest for 1980 and gradually grows towards 2022. Legend also shows mean RMSE improvement (a fraction of RMSE left after DA).

Fig. 9

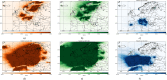
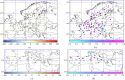
Histograms of correlation coefficient between the observed and predicted/assimilated inter-annual SPIn variations. Three cases are considered: unconstrained reference run, raw output of the DA run, and bias-corrected final run. All years and all stations with >3 years of valid observations are included.

Fig. 10

Quantile plots for assimilated SPIn. The plot is obtained by an independent sorting of the observations and the corresponding model predictions, thus disregarding their temporal co-location and only accounting for the relation between the distribution functions of the observed and predicted concentrations.

Fig. 11

Ratio of observed and modelled multi-annual SPIn.

Fig. 12

Histograms of temporal correlation coefficient between observed and predicted 2-daily-mean pollen concentrations, 1980–2022. The coefficient is computed for each station and for each year.

Fig. 13

Areas observed by the active stations in 1980 (upper row, 1985 for olives) and 2022 (lower row), [relative]. The presented variable is the sum of footprints of all active stations throughout the growth and flowering season 1 January–31 July.

Fig. 14

Bias (left column, panels a,c) and correlation coefficient (right column, panels b,d) of the SILAM birch (upper row, panels a,b) and olive (lower row, panels c, d) forecasts in 2022, as evaluated by Copernicus Atmospheric Monitoring Service. Adopted from CAMS283-2023 report, available for unrestricted use from the CAMS Web portal.