Fast Context-Aware Analysis of Genome Annotation Colocalization

Abstract

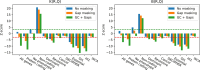
An annotation is a set of genomic intervals sharing a particular function or property. Examples include genes or their exons, sequence repeats, regions with a particular epigenetic state, and copy number variants. A common task is to compare two annotations to determine if one is enriched or depleted in the regions covered by the other. We study the problem of assigning statistical significance to such a comparison based on a null model representing random unrelated annotations. To incorporate more background information into such analyses, we propose a new null model based on a Markov chain that differentiates among several genomic contexts. These contexts can capture various confounding factors, such as GC content or assembly gaps. We then develop a new algorithm for estimating p-values by computing the exact expectation and variance of the test statistic and then estimating the p-value using a normal approximation. Compared to the previous algorithm by Gafurov et al., the new algorithm provides three advances: (1) the running time is improved from quadratic to linear or quasi-linear, (2) the algorithm can handle two different test statistics, and (3) the algorithm can handle both simple and context-dependent Markov chain null models. We demonstrate the efficiency and accuracy of our algorithm on synthetic and real data sets, including the recent human telomere-to-telomere assembly. In particular, our algorithm computed p-values for 450 pairs of human genome annotations using 24 threads in under three hours. Moreover, the use of genomic contexts to correct for GC bias resulted in the reversal of some previously published findings.

Keywords: Markov chains; colocalization; genome annotation.

FIG. 1.

An illustration of an annotation generated by a context-aware Markov chain. Query annotation $Q=\{[1,3),[5,7),[9,14)\}$ is shown as boxes on top of the figure. Genome context $\varphi$ is shown below with black and gray colors corresponding to two distinct class labels. The same colors are also used on transition arrows between successive states of the Markov chain in the bottom part of the figure, as the transition probabilities depend on the genome context. The sequence of states that induce annotation Q is highlighted.

FIG. 2.

An example of a reference annotation R and the corresponding two-sided plumbuses. The plumbuses in the first row correspond to the reference intervals, and the plumbuses in the second row correspond to the gaps between the intervals. For each plumbus, we highlight in black the boundary states on which we condition its values. Note that the conditional means μ_v and variances ${\sigma }_v^2$ in the gap plumbuses are constant zeros since gaps do not contribute to the total test statistic.

FIG. 3.

An example of the decomposition of a single reference interval into single-class two-sided plumbuses used in computation for the shared bases statistic $B(·,·)$. Note that these plumbuses can be computed in time logarithmic in the length of their genomic interval and then merged into a single plumbus for the whole reference interval in time linear in their count (see the proof of Theorem 3). The two class labels are shown as different background colors.

FIG. 4.

The comparison of the exact PMF for the number of overlaps K statistic (MCDP*) with its normal approximation (MCDP2) on synthetic data sets. Each column represents a different number of reference intervals ( $\left|R\right|\in \{200,2000,20000\}$). The top row compares the central part of the two distributions. The middle row shows differences for the extreme tail of the distributions. The curves represent the exact and approximated p-value for different values of the statistic, starting from the position with Z-score +3. Finally, the bottom row contains the quantile–quantile plots (Q–Q plots) between the two distributions. The normal distribution is a very good estimate of the true PMF, except for extreme tails for small values of $\left|R\right|$.

FIG. 5.

The comparison of the exact PMF for the number of shared bases statistic B with its normal approximation on synthetic data sets. Each column represents a different total number of bases in reference intervals ( $B\left(R\right)\in \{200,2000,20000\}$). The top row compares the central part of the exact PMF (labeled “mcdp* unit”) with the normal approximation computed using our new MCDP2 algorithm (labeled “mcdp2 bases”). The middle row shows p-values for the extreme tail of the distribution, starting from the position with Z-score +3. Finally, the bottom row contains the quantile–quantile plots. The center of the distribution is well approximated for $B\left(R\right)\ge 2000$, but the extreme tails differ even for $B(R)=20000$.

FIG. 6.

Average running time on synthetic data for overlaps statistic (MCDP2, MCDP*) and shared bases statistic (MCDP2). The vertical bars represent the standard deviation over 20 samples, which were generated as in Figure 4. Both axes are in log scale. The linear and quasi-linear algorithms of MCDP2 are much faster than quadratic-time MCDP* for large reference annotations. The calculations were performed on a single thread on Intel(R) Xeon(R) Gold 6248R CPU.

FIG. 7.

Z-scores for colocalization of exons of various gene groups (R, x-axis) with copy number losses (Q) under three different null models: single-class context, gap-aware context, and GC-aware context. Left: overlap statistic K; Right: shared bases statistic B. The green and red dashed lines stand for Z-score +3 and −3 respectively, corresponding to p-value of 0.00135 for enrichment/depletion. The context with gaps generally decreases the Z-score, addition of the GC content also significantly influences some of the results.

FIG. 8.

Relative enrichment of epigenetic modifications (Q) in telomere-associated repeats (TARs) located further than 20 kbp from chromosome ends (R₁) in comparison to all TARs (R₂), using both the number of overlaps statistic K (left) and the number of shared bases statistic B (right). The numbers in the parentheses denote the number of cell lines available for each modification. Activating marks H3K27ac and H3K4me3 are enriched in both statistics; CTCF enrichment is more pronounced under the B statistic.