Pangenome comparison via ED strings
- PMID: 39391331
- PMCID: PMC11464492
- DOI: 10.3389/fbinf.2024.1397036
Pangenome comparison via ED strings
Abstract
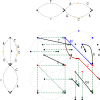
Introduction: An elastic-degenerate (ED) string is a sequence of sets of strings. It can also be seen as a directed acyclic graph whose edges are labeled by strings. The notion of ED strings was introduced as a simple alternative to variation and sequence graphs for representing a pangenome, that is, a collection of genomic sequences to be analyzed jointly or to be used as a reference.
Methods: In this study, we define notions of matching statistics of two ED strings as similarity measures between pangenomes and, consequently infer a corresponding distance measure. We then show that both measures can be computed efficiently, in both theory and practice, by employing the intersection graph of two ED strings.
Results: We also implemented our methods as a software tool for pangenome comparison and evaluated their efficiency and effectiveness using both synthetic and real datasets.
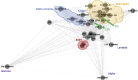
Discussion: As for efficiency, we compare the runtime of the intersection graph method against the classic product automaton construction showing that the intersection graph is faster by up to one order of magnitude. For showing effectiveness, we used real SARS-CoV-2 datasets and our matching statistics similarity measure to reproduce a well-established clade classification of SARS-CoV-2, thus demonstrating that the classification obtained by our method is in accordance with the existing one.
Keywords: SARS-CoV-2; elastic-degenerate string; intersection graph; matching statistics; pangenome comparison.
Copyright © 2024 Gabory, Mwaniki, Pisanti, Pissis, Radoszewski, Sweering and Zuba.
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures
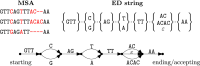
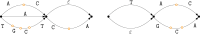

References
-
- Alzamel M., Ayad L. A. K., Bernardini G., Grossi R., Iliopoulos C. S., Pisanti N., et al. (2018). “Degenerate string comparison and applications,”. 18th international workshop on algorithms in bioinformatics, WABI 2018, August 20-22, 2018, Helsinki, Finland. Editors Parida L., Ukkonen E. (Schloss Dagstuhl: LIPIcs; ), 21, 1–21:14. 113 of LIPIcs . 10.4230/LIPIcs.WABI.2018.21 - DOI
-
- Alzamel M., Ayad L. A. K., Bernardini G., Grossi R., Iliopoulos C. S., Pisanti N., et al. (2020). Comparing degenerate strings. Fundam. Inf. 175, 41–58. 10.3233/FI-2020-1947 - DOI
-
- Aoyama K., Nakashima Y., I T., Inenaga S., Bannai H., Takeda M. (2018). “Faster online elastic degenerate string matching,”. Annual symposium on combinatorial pattern matching, CPM 2018, july 2-4, 2018 - qingdao, China. Editors Navarro G., Sankoff D., Zhu B. (Schloss Dagstuhl: LIPIcs; ), 9, 1–9:10. 10.4230/LIPIcs.CPM.2018.9 - DOI
-
- Apostolico A., Guerra C., Landau G. M., Pizzi C. (2016). Sequence similarity measures based on bounded hamming distance. Theor. Comput. Sci. 638, 76–90. 10.1016/J.TCS.2016.01.023 - DOI
-
- Apostolico A., Guerra C., Pizzi C. (2014). “Alignment free sequence similarity with bounded hamming distance,” in Data compression conference, DCC 2014, snowbird, UT, USA, 26-28 march, 2014. Editors Bilgin A., Marcellin M. W., Serra-Sagristà J., Storer J. A. (IEEE; ), 183–192. 10.1109/DCC.2014.57 - DOI
LinkOut - more resources
Full Text Sources
Research Materials
Miscellaneous

