Generalised Entropy Accumulation

Abstract

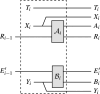
Consider a sequential process in which each step outputs a system $A_i$ and updates a side information register E. We prove that if this process satisfies a natural "non-signalling" condition between past outputs and future side information, the min-entropy of the outputs $A_1,\cdots ,A_n$ conditioned on the side information E at the end of the process can be bounded from below by a sum of von Neumann entropies associated with the individual steps. This is a generalisation of the entropy accumulation theorem (EAT) (Dupuis et al. in Commun Math Phys 379: 867-913, 2020), which deals with a more restrictive model of side information: there, past side information cannot be updated in subsequent rounds, and newly generated side information has to satisfy a Markov condition. Due to its more general model of side-information, our generalised EAT can be applied more easily and to a broader range of cryptographic protocols. As examples, we give the first multi-round security proof for blind randomness expansion and a simplified analysis of the E91 QKD protocol. The proof of our generalised EAT relies on a new variant of Uhlmann's theorem and new chain rules for the Rényi divergence and entropy, which might be of independent interest.

Fig. 1

Circuit diagram of $\mathcal{N}:R_{i-1}{E}_{i-1}^{\prime }\to A_i{R}_i{T}_i{X}_i{Y}_i{B}_i{E}_i^{\prime }$. For every round of the protocol, a circuit of this form is applied, where $\mathcal{A}$ and $\mathcal{B}$ are the (arbitrary) channels applied by Alice’s device and Eve, respectively. As in the protocol, $T_i$ is a bit equal to 1 with probability $\gamma$, and $X_i$ and $Y_i$ are generated according to q whenever $T_i=1$, and are fixed to $x^{\ast },y^{\ast }$ otherwise. We did not include the register $C_i$ in the figure as it is a deterministic function of $T_i{X}_i{Y}_i{A}_i{B}_i$

Fig. 2

Lower bound on the conditional entropy $H{(A_i|B_i{X}_i{Y}_i{T}_i{E}_i^{\prime })}_{{\rho }_{|T_i=0}}$ for any state generated as in Fig. 1 and such that on test rounds the obtained winning probability for the CHSH game is $\omega$. This lower bound was obtained by using the method from [22]. For each input $y\in \mathcal{Y}$, the channel ${\mathcal{B}}_y$ is modelled as ${\mathcal{B}}_y(\omega )={\sum }_b{\mathrm{\Pi }}_y^{(b)}\omega {\mathrm{\Pi }}_y^{(b)}$, where ${\{{\mathrm{\Pi }}_y^{(b)}\}}_{b\in \mathcal{B}}$ are orthogonal projectors summing to the identity, and similarly for the map $\mathcal{A}$. It is simple to see that this is without loss of generality