Rydberg-State Double-Well Potentials of Van der Waals Molecules
- PMID: 39407588
- PMCID: PMC11477599
- DOI: 10.3390/molecules29194657
Rydberg-State Double-Well Potentials of Van der Waals Molecules
Abstract
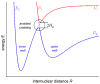
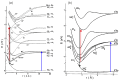
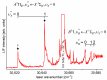
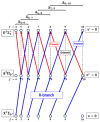
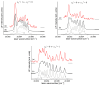
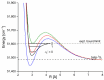
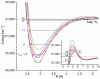
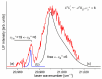
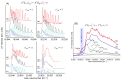
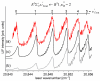
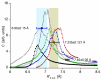
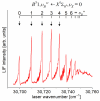
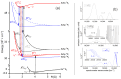
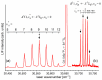
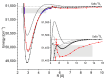
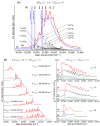
Recent progress in studies of Rydberg double-well electronic energy states of MeNg (Me = 12-group atom, Ng = noble gas atom) van der Waals (vdW) molecules is presented and analysed. The presentation covers approaches in experimental studies as well as ab initio-calculations of potential energy curves (PECs). The analysis is shown in a broader context of Rydberg states of hetero- and homo-diatomic molecules with PECs possessing complex 'exotic' structure. Laser induced fluorescence (LIF) excitation spectra and dispersed emission spectra employed in the spectroscopical characterization of Rydberg states are presented on the background of the diverse spectroscopic methods for their investigations such as laser vaporization-optical resonance (LV-OR), pump-and-probe methods, and polarization labelling spectroscopy. Important and current state-of-the-art applications of Rydberg states with irregular potentials in photoassociation (PA), vibrational and rotational cooling, molecular clocks, frequency standards, and molecular wave-packet interferometry are highlighted.
Keywords: Rydberg electronic state; ab initio calculations; double-well potential; rotational energy structure; van der Waals molecule; vibrational energy structure.
Conflict of interest statement
The authors declare no conflicts of interest.
Figures
















Similar articles
-
Observation of gerade Rydberg state of Cd2 van der Waals complex cooled in free-jet expansion beam and excited using optical-optical double resonance method.Spectrochim Acta A Mol Biomol Spectrosc. 2021 May 15;253:119500. doi: 10.1016/j.saa.2021.119500. Epub 2021 Feb 4. Spectrochim Acta A Mol Biomol Spectrosc. 2021. PMID: 33611214
-
Rotational characterization of the E3Σ1+(5s6s 3S1) Rydberg state of CdNe van der Waals complex via selective J-excitation in OODR process.Spectrochim Acta A Mol Biomol Spectrosc. 2022 Jan 5;264:120248. doi: 10.1016/j.saa.2021.120248. Epub 2021 Aug 8. Spectrochim Acta A Mol Biomol Spectrosc. 2022. PMID: 34391062
-
The structure of the lowest electronic Rydberg state of CdAr complex determined by laser double resonance method in a supersonic jet-expansion beam.Spectrochim Acta A Mol Biomol Spectrosc. 2003 Sep;59(11):2435-48. doi: 10.1016/s1386-1425(02)00396-7. Spectrochim Acta A Mol Biomol Spectrosc. 2003. PMID: 12963441
-
The lowest-lying Rydberg state of CdAr van der Waals complex: The improved characterization of the interatomic potential.Spectrochim Acta A Mol Biomol Spectrosc. 2022 Dec 5;282:121655. doi: 10.1016/j.saa.2022.121655. Epub 2022 Jul 21. Spectrochim Acta A Mol Biomol Spectrosc. 2022. PMID: 35964381
-
Rydberg Macrodimers: Diatomic Molecules on the Micrometer Scale.J Phys Chem A. 2023 May 11;127(18):3925-3939. doi: 10.1021/acs.jpca.2c08454. Epub 2023 Mar 28. J Phys Chem A. 2023. PMID: 36977279 Free PMC article. Review.
References
-
- von Neumann J., Wigner E.P. Über das Verhalten von Eigenwerten bei adiabatischen Prozessen. Phys. Z. 1929;30:467–479. doi: 10.1007/978-3-662-02781-3_20. - DOI
-
- Dressler K. In: Photophysics and Photochemistry above 6 eV. Lahmani F., editor. Elsevier; Amsterdam, The Netherlands: 1985. pp. 327–341.
-
- Kędziorski A., Zobel J.P., Krośnicki M., Koperski J. Rydberg states of ZnAr complex. Mol. Phys. 2022;120:e2073282. doi: 10.1080/00268976.2022.2073282. - DOI
-
- Krośnicki M., Kędziorski A., Urbańczyk T., Koperski J. Rydberg states of the CdAr van der Waals complex. Phys. Rev. A. 2019;99:052510. doi: 10.1103/PhysRevA.99.052510. - DOI
-
- Czuchaj E., Krośnicki M., Stoll H. Quasirelativistic valence ab initio calculation of the potential curves for the Zn-rare gas van der Waals molecules. Chem. Phys. 2001;265:291–299. doi: 10.1016/S0301-0104(01)00323-8. - DOI
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources

