Harmonic Vibration Analysis in a Simplified Model for Monitoring Transfemoral Implant Loosening

Abstract

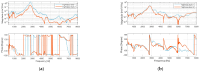
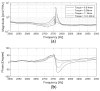
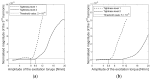
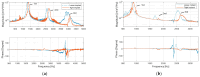
A simplified axisymmetric model of a transfemoral osseointegration implant was used to investigate the influence of the contact condition at the bone-implant interface on the vibrational response. The experimental setup allowed the degree of implant tightness to be controlled using a circumferential compression device affixed to the bone. Diametrically placed sensors allowed torsional modes to be distinguished from flexural modes. The results showed that the structural resonant frequencies did not shift significantly with tightness levels. The first torsional mode of vibration was found to be particularly sensitive to interface loosening. Harmonics in the vibrational response became prominent when the amplitude of the applied torque increased beyond a critical level. The torque level at which the third harmonic begins to rise correlated with implant criticality, suggesting a potential strategy for early detection of implant loosening based on monitoring the amplitude of the third harmonic of the torsional mode.

Keywords: bone–implant interface; osseointegration implant loosening; structural health monitoring; vibrational analysis.

Figure 1

Experimental setup for the nonlinear vibration test.

Figure 2

The implants were excited by a random signal from 300 Hz to 10,000 Hz. (a) Magnitude spectrum and phase spectrum of the cross power spectral density between acceleration s1 and s2. (b) Magnitude spectrum and phase spectrum of the frequency response function between acceleration s1 and s4.

Figure 3

Time history and Fast Fourier Transform (FFT) of accelerations s1 and s3 for the experimental setup at tightness level 1, subject to excitation torques of (a) 5.6 Nmm, (b) 6.6 Nmm, (c) 7.2 Nmm, (d) 9.2 Nmm, (e) 11 Nmm, and (f) 12.3 Nmm.

Figure 4

Magnitude spectrum (a) and phase spectrum (b) of the Frequency Response Function for acceleration s1 (excitation signal) and s3 (response signal) when the implant, tightened to level 1, was excited at its resonance of 2760 Hz.

Figure 5

Changes in the magnitude of the third harmonics in the normalised auto-power spectrum density of (a) accelerations s1 and (b) accelerations s3.

Figure 6

The magnitude of the third harmonic in the auto-spectrum of (a) accelerations s1 and (b) accelerations s3, as a function of α $={\displaystyle \frac{{\mathrm{T}}_{\mathrm{E}}}{{\mathrm{T}}_{\mathrm{C}}}}$, where ${\mathrm{T}}_{\mathrm{E}}$ is the amplitude of the excitation torque and ${\mathrm{T}}_{\mathrm{C}}$ is the amplitude of the load capacity determined through a threshold value, as shown in Figure 5.

Figure 7

Magnitude and phase spectrum of the cross-power spectrum between acceleration s1 and s3: (a) The loose and tight implants were excited with the same voltage level at half (around 1400 Hz) the resonance. (b) The loose and tight implants were excited with the same voltage level at one third (around 700 Hz) of the resonance.

Figure 8

(a) The two-dimensional contact model which aims to simulate a representative cross section A–A of the contact region as shown in (b).

Figure 9

(a) Time history of the contact friction stress. (b) Time history of the acceleration probed at sensor s1 for different excitation levels (6 Nmm, 8 Nmm, 11 Nmm). (c) Normalised auto-power spectrum density of accelerations.

Figure 10

Evolution of (a) the second, and (b) the third harmonic amplitudes in the auto-power spectrum density of s1.

Figure 11

Interfacial contact models that are symmetrical with respect to relative displacement across the interface: (a) Coulomb friction model; (b) linear sliding contact model terminated by frictional sliding, where µ is the friction coefficient and N is the normal contact force.