Correlated topological flat bands in rhombohedral graphite

Abstract

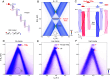
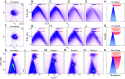
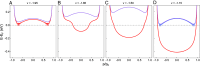
Flat bands and nontrivial topological physics are two important topics of condensed matter physics. With a unique stacking configuration analogous to the Su-Schrieffer-Heeger model, rhombohedral graphite (RG) is a potential candidate for realizing both flat bands and nontrivial topological physics. Here, we report experimental evidence of topological flat bands (TFBs) on the surface of bulk RG, which are topologically protected by bulk helical Dirac nodal lines via the bulk-boundary correspondence. Moreover, upon in situ electron doping, the surface TFBs show a splitting with exotic doping evolution, with an order-of-magnitude increase in the bandwidth of the lower split band, and pinning of the upper band near the Fermi level. These experimental observations together with Hartree-Fock calculations suggest that correlation effects are important in this system. Our results demonstrate RG as a platform for investigating the rich interplay between nontrivial band topology, correlation effects, and interaction-driven symmetry-broken states.

Keywords: correlated efffects; helical Dirac nodal lines; rhombohedral graphite; topological flat bands.

Fig. 1.

Schematic illustration of RG, surface topological flat bands (surface TFBs) and bulk helical Dirac nodal lines (bulk helical DNLs), and experimental observations. (A) Schematic illustration of the atomic structure of bulk RG (side view), which is analogous to the SSH model (Inset in the Lower Left corner). (B) Calculated electronic spectral weight for RG with N = 70 layers. The surface TFBs are indicated by the red arrow, while the light-blue colors arise from the bulk conical bands. (C) Schematic illustration of the surface TFBs (red and blue ovals) and bulk helical DNLs (red and blue helixes). (D) ARPES dispersion image measured by cutting through the K point as indicated by the Inset. (E and F) Dispersion images measured upon low and high electron doping, respectively. The splitting of the TFBs is indicated by red and orange arrows, and the lower split band is denoted by LB.

Fig. 2.

Observation of surface TFBs and bulk Dirac node. (A–F) ARPES-measured intensity maps at a few representative energies from E_F to −0.30 eV measured on sample S2. The photon energy used is 60 eV, which corresponds to $k_z=0.11 c^{\ast }$ in the reduced BZ ($c^{\ast }=\frac{2\pi }{c}$, where $c=$ 3.34Å is the out-of-plane lattice constant) for the K point. The red arrow indicates the TFBs and the blue arrow in (D) indicates the bulk Dirac node (bulk DN). (G–P) Dispersion images measured by cutting through the K point along different directions indicated by arrows in the Insets. (Q) Schematic summary of the experimental electronic structure, including the DN (blue color) and the TFBs near E_F (red color).

Fig. 3.

Observation of bulk helical DNLs and surface TFBs along the out-of-plane momentum direction. (A–N) Energy contours measured at −50 meV at photon energies from 40 eV to 105 eV to show the rotation of the Dirac node as indicated by pink arrows. The Dirac node is barely detectable at $80 \text{eV} \text{to} 95 \text{eV}$ due to suppression of the intensity by dipole matrix element effects. (O) Energy contours around the K point measured at −100 meV at photon energies from 40 eV (Bottom) to 105 eV (Top), which correspond to reduced k_z values from $1.72c^{\ast }$ to $2.79c^{\ast }$. (P) Schematic drawing of helical DNL around the K^′ point, which exhibits the opposite chirality to that in the K point. (Q–V) Dispersion images measured at photon energies from 40 eV to 105 eV to reveal the nondispersive TFBs indicated by red arrows. All dispersion images were measured by cutting through the Dirac node and K point at each photon energy, as indicated in the Insets.

Fig. 4.

Correlated evolution of the surface TFBs electronic structure upon in situ electron doping. (A) Fermi surface map measured before electron doping. (B–E) ARPES dispersion images cutting along the k_y direction as indicated by gray broken lines in (A). (F) Fermi surface map measured at low electron doping. (G–J) ARPES dispersion images cutting along the k_y direction as indicated by gray broken lines in (F). (K–O) ARPES Dispersion images cutting through the K point along k_y direction upon electron doping. (P–R) Schematics for the undoped electronic structure, flavor splitting of TFBs, and an increase in bandwidth of the lower band upon electron doping, where orange and red colors indicate the Upper and Lower split TFBs respectively. The measurements here were performed on sample S1.

Fig. 5.

Hartree–Fock band structures at negative fillings. (A–D) Self-consistent Hartree–Fock calculations of the surface TFBs at fillings of $\nu =-1.95$, $-1.85$, $-1.50$, and $-1.15$, respectively. Each panel shows the four resulting Hartree–Fock bands. The Top three bands are degenerate. The Bottom of the lowest TFB (red curve) moves from near the Fermi level to approximately $-400 \text{meV}$ (see SI Appendix, Fig. S10 for similar plots at fillings of $\nu =-1.0$, $-0.8$, $-0.4$, and $0.0$).