k-nonical space: sketching with reverse complements
- PMID: 39432565
- PMCID: PMC11549021
- DOI: 10.1093/bioinformatics/btae629
k-nonical space: sketching with reverse complements
Abstract
Motivation: Sequences equivalent to their reverse complements (i.e. double-stranded DNA) have no analogue in text analysis and non-biological string algorithms. Despite this striking difference, algorithms designed for computational biology (e.g. sketching algorithms) are designed and tested in the same way as classical string algorithms. Then, as a post-processing step, these algorithms are adapted to work with genomic sequences by folding a k-mer and its reverse complement into a single sequence: The canonical representation (k-nonical space).
Results: The effect of using the canonical representation with sketching methods is understudied and not understood. As a first step, we use context-free sketching methods to illustrate the potentially detrimental effects of using canonical k-mers with string algorithms not designed to accommodate for them. In particular, we show that large stretches of the genome ("sketching deserts") are undersampled or entirely skipped by context-free sketching methods, effectively making these genomic regions invisible to subsequent algorithms using these sketches. We provide empirical data showing these effects and develop a theoretical framework explaining the appearance of sketching deserts. Finally, we propose two schemes to accommodate for these effects: (i) a new procedure that adapts existing sketching methods to k-nonical space and (ii) an optimization procedure to directly design new sketching methods for k-nonical space.
Availability and implementation: The code used in this analysis is available under a permissive license at https://github.com/Kingsford-Group/mdsscope.
© The Author(s) 2024. Published by Oxford University Press.
Figures
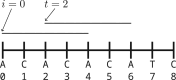
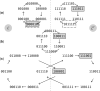
References
-
- Axler S. Linear Algebra Done Right. Springer Nature, 2015.
-
- Champarnaud J-M, Hansel G, Perrin D.. Unavoidable sets of constant length. Int J Algebra Comput 2004;14:241–51. 10.1142/S0218196704001700 - DOI
-
- DeBlasio D, Gbosibo F, Kingsford C. et al. Practical universal k-mer sets for minimizer schemes. In Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, BCB ’19, pp. 167–76. New York, NY, USA: ACM, 2019.
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
Miscellaneous

