Vector time series modelling of turbidity in Dublin Bay

Abstract

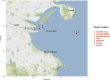
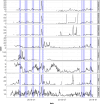
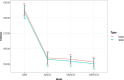
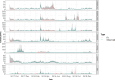
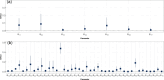
Turbidity is commonly monitored as an important water quality index. Human activities, such as dredging and dumping operations, can disrupt turbidity levels and should be monitored and analysed for possible effects. In this paper, we model the variations of turbidity in Dublin Bay over space and time to investigate the effects of dumping and dredging while controlling for the effect of wind speed as a common atmospheric effect. We develop a Vector Auto-Regressive Integrated Conditional Heteroskedasticity (VARICH) approach to modelling the dynamical behaviour of turbidity over different locations and at different water depths. We use daily values of turbidity during the years 2017-2018 to fit the model. We show that the results of our fitted model are in line with the observed data and that the uncertainties, measured through Bayesian credible intervals, are well calibrated. Furthermore, we show that the daily effects of dredging and dumping on turbidity are negligible in comparison to that of wind speed.

Keywords: Bayesian; turbidity; vector autoregression.

Figure 1.

Buoys measuring turbidity in Dublin Bay. We use the same numbering scheme when referring to each site throughout the paper. Buoys 4 to 7 are potential dredging sites, whilst the sediment is dumped at the dumpsite.

Figure 2.

Daily measurements of turbidity (NTU) at Tolka, Eastlink, Poolbeg, Northbank, and various depths of the dumpsite, alongside wind speed (knots) measurements, from 31 August 2017 to 31 December 2018. The highlighted regions indicate the periods during which dredging and dumping operations occurred.

Figure 3.

WAIC and LOOIC values for the four fitted models with their associated standard errors.

Figure 4.

Posterior prediction from the VARICH model vs observed values of turbidity over time for the 7 buoys as labelled. Note the differing vertical axis heights. The shaded periods indicate 95% credible intervals.

Figure 5.

Fitted values from the VARICH model versus observed values of turbidity at different sites. The vertical bars indicate the 95% uncertainty intervals which provide evidence of the coverage properties of the model.

Figure 6.

Dumping and dredging effects (NTU/day) at different locations with the 95% credible interval.

Figure 7.

Effect of wind speed (NTU/Knot) at different locations and depths with the 95% credible interval.

Figure 8.

Coefficients of the Φ matrix with their 95% credible interval. Diagonal values are shown in the top panel (a) and off-diagonal values are shown in (b). The two subscripts indicate the parent and child relationship respectively, so that ${\mathrm{\Phi }}_{12}$ for example is the degree to which buoy 2 influences the time series of buoy 1. The numbers of the buoys follow the labelling defined in Figure 1.