Leveraging information from secondary endpoints to enhance dynamic borrowing across subpopulations

Abstract

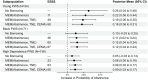
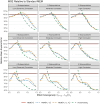
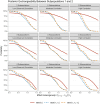
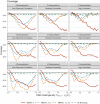
Randomized trials seek efficient treatment effect estimation within target populations, yet scientific interest often also centers on subpopulations. Although there are typically too few subjects within each subpopulation to efficiently estimate these subpopulation treatment effects, one can gain precision by borrowing strength across subpopulations, as is the case in a basket trial. While dynamic borrowing has been proposed as an efficient approach to estimating subpopulation treatment effects on primary endpoints, additional efficiency could be gained by leveraging the information found in secondary endpoints. We propose a multisource exchangeability model (MEM) that incorporates secondary endpoints to more efficiently assess subpopulation exchangeability. Across simulation studies, our proposed model almost uniformly reduces the mean squared error when compared to the standard MEM that only considers data from the primary endpoint by gaining efficiency when subpopulations respond similarly to the treatment and reducing the magnitude of bias when the subpopulations are heterogeneous. We illustrate our model's feasibility using data from a recently completed trial of very low nicotine content cigarettes to estimate the effect on abstinence from smoking within three priority subpopulations. Our proposed model led to increases in the effective sample size two to four times greater than under the standard MEM.

Keywords: Bayesian model averaging; basket trials; dynamic borrowing; multisource exchangeability models; secondary endpoints; subpopulation analysis.

FIGURE 1

Posterior means, 95% credible intervals (CIs), and effective supplementary sample sizes (ESSSs) for absolute risk difference on abstinence from smoking (VLNC group − normal nicotine content group) within the three subpopulations of interest under each considered model.

FIGURE 2

Pairwise exchangeability probabilities between all subpopulations.

FIGURE 3

Relative mean squared error (MSE) estimating subpopulation treatment effects across models with 200 subjects per subpopulation. MSE is presented relative to the MEM that only considered the primary endpoint []. (Note that the upper limit of the vertical axis has been truncated to 110% for visual clarity; the relative average mean squared error for “No Borrowing” extends as high as 200% when all subpopulations have the same treatment effect.)

FIGURE 4

Posterior probabilities of exchangeability between subpopulations 1 and 2 as a function of the difference in subpopulation average treatment effects with 200 subjects per subpopulation.

FIGURE 5

Median effective supplementary sample size across all subpopulations as a function of the difference in subpopulation average treatment effects with 200 subjects per subpopulation.

FIGURE 6

Average coverage of 95% credible intervals across all subpopulations as a function of the difference in subpopulation average treatment effects with 200 subjects per subpopulation.