Anomalous frozen evanescent phonons

Abstract

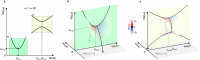
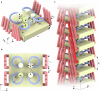
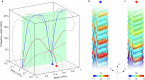
Evanescent Bloch waves are eigensolutions of spatially periodic problems for complex-valued wavenumbers at finite frequencies, corresponding to solutions that oscillate in time and space and that exponentially decay in space. Such evanescent waves are ubiquitous in optics, plasmonics, elasticity, and acoustics. In the limit of zero frequency, the wave "freezes" in time. We introduce frozen evanescent waves as the eigensolutions of the Bloch periodic problem at zero eigenfrequency. Elastic waves, i.e., phonons, in metamaterials serve as an example. We show that, in the complex plane, the Cauchy-Riemann equations for analytical functions connect the minima of the phonon band structure to frozen evanescent phonons. Their exponential decay length becomes unusually large if a minimum in the band structure tends to zero and thereby approaches a soft mode. This connection between unusual static and dynamic behaviors allows to engineer large characteristic decay lengths in static elasticity. For finite-size samples, the static solutions for given boundary conditions are linear combinations of frozen evanescent phonons, leading to interference effects. Theory and experiment are in excellent agreement. Anomalous behavior includes the violation of Saint Venant's principle, which means that large decay-length frozen evanescent phonons can potentially be applied in terms of remote mechanical sensing.

Fig. 1. Complex-valued band structures and frozen evanescent Bloch modes.

A linear, passive, and lossless infinite periodic system is considered. a Two possible scenarios of dispersion relations, exhibiting local extrema of the real part of the eigenfrequency, $\mathrm{Re}\left(\omega \right)>0$, versus the real part of the wavenumber, $\mathrm{Re}\left(k\right)>0$. The green and yellow colors refer to panels b and c, respectively. b Real part of the eigenfrequency versus real and imaginary part of the wavenumber for the scenario highlighted in green in (a). The black curves correspond to $\mathrm{Im}\left(\omega \right)=0$. The imaginary part of $\omega$ is false-color coded. Two evanescent branches with $\mathrm{Im}\left(k\right)\ne 0$ emerge from the local minimum of $\mathrm{Re}\left(\omega \right)$ versus $\mathrm{Re}\left(k\right)$ (green plane) and touch the $\omega =0$ plane (gray plane). These static or frozen eigenmodes are highlighted by the two black dots. For $\mathrm{Re}\left(k\right)<0$, two further such modes occur. The characteristic exponential decay length of these frozen modes is given by $l=1/\mid \mathrm{Im}\left(k\right)\mid$, their spatial oscillation period by $p=2\pi /\mathrm{Re}\left(k\right)$. c Same as panel b, but for the scenario highlighted in yellow in panel a. Here, no evanescent zero-frequency Bloch modes result.

Fig. 2. Blueprint of metamaterial supporting anomalous frozen evanescent phonons.

This nonlocal mechanical metamaterial composed of a single constituent polymer material allows obtaining frozen evanescent Bloch modes with large characteristic exponential decay length $l$ (cf. Fig. 1b). a, b Two different views onto a single unit cell. The geometrical parameters are defined. Two of the yellow cylinders are rendered semi-transparent to indicate the height of blue helices. The colors are for illustration only. c Beam composed of a one-dimensional periodic arrangement of this unit cell along the $z$-direction with period $a_z$. Adjacent yellow plates are connected by four blue helices (“springs”), fixed to the plates by yellow cylinders. The handedness of the springs alternates, such that the overall structure has two mirror planes, making it achiral. The strength of this nearest-neighbor interaction can be tailored by the radius $R_1$. The yellow plates are additionally connected to their $N$-th neighbors by the red rods with radius $R_N$. This radius determines the strength of the $N$-th nearest neighbor interactions. The example shown refers to $N=3$. We will discuss $N=2,3,4$ with different geometrical parameters. The geometric parameters for $N=2,3,$ and $4$ are chosen as $2R_1/a_z=0.10$, $2R_N/a_z=0.156$, $2R_1/a_z=0.10$, $2R_N/a_z=0.16$, and $2R_1/a_z=0.072$, $2R_N/a_z=0.10$, respectively. All other geometrical parameters are fixed: $a_z=100\mathrm{\mu m}$, $2R_1/a_z=0.10$, $2R_N/a_z=0.16$, $w/a_z=2.0,h/a_z=0.34$, $h_1/a_z=0.16$, $h_2/a_z=0.34$, $h_3/a_z=0.50$, $D_1/a_z=0.30$, $D_2/a_z=0.60$, $L_1/a_z=0.57$, $L_2/a_z=0.30$, and $L_3/a_z=0.70$. For the material parameters of the constituent polymer, we choose mass density $\rho =1190\mathrm{kg}/{\mathrm{m}}^3$, Young’s modulus $E=4.19\mathrm{GPa}$, and Poisson’s ratio $v=0.3$.

Fig. 3. Complex-valued phonon band structure and frozen evanescent phonon modes.

a Numerically calculated phonon band structure for elastic-wave propagation in the metamaterial beam ($N=3$) defined in Fig. 2 for wave propagation along the $z$-direction. The representation is as in Fig. 1b, except that only real-valued frequencies are depicted, $\mathrm{Im}\left(\omega \right)=0$. Out of many modes (gray), two are highlighted. The blue modes correspond to longitudinal waves, and the red modes to twist waves. Out of the corresponding local minima in the green plane, evanescent modes emerge (cf. Fig. 1b) that touch the $\omega =0$ plane at the positions of the colored dots. For the longitudinal mode (blue dot) relevant to the below experiments, we find the complex-valued wavenumber $k_z\approx \left(0.666-0.026\mathrm{i}\right)\pi /a_z$. Similar band structures are shown in Supplementary Fig. 1 for $N=2$ and $N=4$. b Illustration of this frozen mode. The axial component of the displacement vector, $u_z$, is depicted in a false-color representation. The static spatial oscillation period of $p=2\pi /\mathrm{Re}\left(k_z\right)\approx N{a}_z=3a_z$ is clearly visible. The mode exponentially decays with decay length $l=1/\mid \mathrm{Im}\left(k_z\right)\mid$. c Same as panel (b), but for the zero-frequency twist mode (red dot in a), with an azimuthal component of the displacement vector $u_{\theta }$.

Fig. 4. Image gallery of manufactured samples.

Following the blueprint shown in Fig. 2 and for the experiments shown in Fig. 5, we have manufactured a total of 10 different polymer samples on glass substrates with different nonlocal orders of interaction $N=2,3,4$, different relative lengths $L/a_z=37,38,39,40$, and for realizing two different loading conditions. a–c oblique-view scanning-electron micrographs. A spring (rod) mediating the local (nonlocal) interactions is highlighted in blue (red). d–f optical micrographs. Panel (d) shows the overall sample with length $L$, and panels (e) and (f) show the hook used for stretching the samples.

Fig. 5. Anomalous displacement fields of stretched metamaterial beams.

a Side-view optical micrograph of a metamaterial beam sample (also see Fig. 2 and Fig. 4) extending from $z=0$ (glass-substrate side) to $z=L$. b Simplified representation in terms of a mass-and-spring model. c A force along the $z$-direction is exerted at the last unit cell of the samples at $z=L$, leading to a stretching of the samples along the $z$-direction by an engineering strain of $u_{\max }/L\approx 1\%$. The resulting displacement-vector component $u_z$ is recorded as a function of the site number or relative position $z/a_z$. Orange dots refer to experimental measurements, blue dots refer to finite-element numerical calculations, and red dots to solutions of the mass-and-spring model. We note that the finite-element results largely overlap with the other data within the symbol size, indicating excellent agreement. The integer parameters $N$ and $L_z/a$ are indicated in the subpanels. For an ordinary elastic material, the displacement field would simply follow $u_z\left(z\right)=u_{\max }z/L$. We rather find pronounced oscillations of $u_z\left(z\right)$ that depend on the parameters $N$ and on $L/a_z$. d As $N=2$ and $L/a_z$ in panel (c), but the force is applied at the two last unit cells simultaneously.

Fig. 6. Decomposition of displacement field.

a Result for the case of $N=2$ and $L/a_z=39$ in Fig. 5c. The total displacement (cf. red dots) is the solution of the mass-and-spring model shown in Fig. 5b. It is composed of a non-Bloch part $u_z^{\mathrm{nB}}=c_1+c_{2}z$ (cf. gray dots), a frozen evanescent phonon eigensolution localized to the left end (cf. green dots), and a frozen evanescent phonon eigensolution localized to the right end (cf. purple dots) of the finite-length beam, respectively. See Methods for details on the decomposition. The two frozen evanescent phonon eigensolutions exhibit in-phase displacement fields in the middle of the beam, leading to constructive interference in the middle (cf. red dots). The straight lines connecting the dots are merely a guide to the eye. b Same as (a) but for $N=2$, $L/a_z=40$. Here, the total displacement (cf. red dots) in the middle shows a smaller oscillation amplitude than in (a) due to the destructive interference of the two frozen evanescent phonon eigensolutions. c Same as (a), but for $N=2$, $L/a_z=40$ under the two-site loading condition (cf. Fig. 5d). This boundary condition significantly suppresses the frozen evanescent phonon to the right end of the beam. See Supplementary Figs. 2 and 3 for other examples ($N=3$, $4$) corresponding to Fig. 5c.