Computation noise promotes zero-shot adaptation to uncertainty during decision-making in artificial neural networks
- PMID: 39475619
- PMCID: PMC11524185
- DOI: 10.1126/sciadv.adl3931
Computation noise promotes zero-shot adaptation to uncertainty during decision-making in artificial neural networks
Abstract
Random noise in information processing systems is widely seen as detrimental to function. But despite the large trial-to-trial variability of neural activity, humans show a remarkable adaptability to conditions with uncertainty during goal-directed behavior. The origin of this cognitive ability, constitutive of general intelligence, remains elusive. Here, we show that moderate levels of computation noise in artificial neural networks promote zero-shot generalization for decision-making under uncertainty. Unlike networks featuring noise-free computations, but like human participants tested on similar decision problems (ranging from probabilistic reasoning to reversal learning), noisy networks exhibit behavioral hallmarks of optimal inference in uncertain conditions entirely unseen during training. Computation noise enables this cognitive ability jointly through "structural" regularization of network weights during training and "functional" regularization by shaping the stochastic dynamics of network activity after training. Together, these findings indicate that human cognition may ride on neural variability to support adaptive decisions under uncertainty without extensive experience or engineered sophistication.
Figures





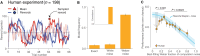
References
-
- Wyart V., Koechlin E., Choice variability and suboptimality in uncertain environments. Curr. Opin. Behav. Sci. 11, 109–115 (2016).
-
- Findling C., Wyart V., Computation noise in human learning and decision-making: Origin, impact, function. Curr. Opin. Behav. Sci. 38, 124–132 (2021).
-
- van Vugt B., Dagnino B., Vartak D., Safaai H., Panzeri S., Dehaene S., Roelfsema P. R., The threshold for conscious report: Signal loss and response bias in visual and frontal cortex. Science 360, 537–542 (2018). - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

