A New Intraocular Lens Power Formula Integrating an Artificial Intelligence-Powered Estimation for Effective Lens Position Based on Chinese Eyes

Abstract

Purpose: To develop and evaluate a new intraocular lens (IOL) formula based on Chinese eyes.

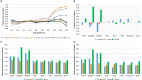
Methods: A training dataset of 709 eyes undergoing uneventful cataract surgery was used to train the algorithm for effective lens position estimation. The algorithm was then integrated with Gaussian optics to develop the new IOL formula (Jin-AI). From the same center, 177 eyes served as an internal test dataset. An independent dataset of 557 eyes served as an external test dataset. The standard deviation (SD) of prediction errors was compared among the Jin-AI formula, traditional third-generation formulas (SRK/T, Holladay 1, Hoffer Q), and newer generation formulas (Kane, Barrett Universal II [BUII], Hill-radial basis function [RBF] 3.0, and PEARL-DGS).

Results: In the internal test dataset, the Jin-AI formula showed the lowest SD (0.25 D), followed by the BUII (0.31 D), Kane (0.33 D), and PEARL-DGS (0.33 D) formulas. In the external test dataset, the Jin-AI, Kane, and PEARL-DGS formulas had the lowest SD (0.38 D), followed by the BUII (0.39 D), Hill-RBF 3.0 (0.39 D), SRK/T (0.45 D), Holladay 1 (0.48 D), and Hoffer Q (0.48 D) formulas. The SD of the Jin-AI formula was significantly lower than the third-generation formulas and comparable to the four newer generation formulas. Predictive accuracy of the Jin-AI formula was similar to the newer generation formulas across all axial length, keratometry, and anterior chamber depth ranges.

Conclusions: The new formula has exhibited good performance in predicting postoperative refractions. Its overall predictive accuracy was better than the third-generation formulas and comparable to the newer generation ones.

Translational relevance: The Jin-AI formula could be a reliable alternative for IOL power calculation in Chinese.

Figure 1.

Block diagram of the Jin-AI formula. The calculation processes highlighted by the dotted green line were used only during development of the algorithm. AL, axial length (mm); ACD, anterior chamber depth (mm); ELP, effective lens position (mm); IOL_power, intraocular lens power (D); n, refractive index of aqueous and vitreous (1.336); n_c, fictitious refractive index of the cornea (1.333); K1, flat keratometry (D); K2, steep keratometry (D); Km, mean keratometry (D); LT, lens thickness (mm); r, corneal radius of curvature (mm); r = 337.5/Km (mm); Rx, postoperative refraction (D); V, vertex distance (12 mm).

Figure 2.

(A) Box plot graph of absolute prediction errors of the eight IOL formulas in total. Blue boxes represent the second quartile, and green boxes represent the third quartile. (B) Stacked histogram comparing the percentage of eyes within prediction error of absolute prediction errors of the eight IOL formulas in total. RBF, Hill–RBF 3.0.

Figure 3.

(A) Line graph comparing the prediction error of the eight IOL formulas versus axial length. (B–D) Prediction error (B), mean absolute prediction error (C), and median absolute prediction error (D) plotted against axial length for the eight IOL formulas.

Figure 4.

(A, B) Line graphs comparing the prediction error of the eight IOL formulas versus keratometry (A) and anterior chamber depth (B). (C, D) Mean absolute prediction error (C) and median absolute prediction error (D) plotted against keratometry for the eight IOL formulas.