Learning-assisted optimization for transmission switching
- PMID: 39479300
- PMCID: PMC11519114
- DOI: 10.1007/s11750-024-00672-0
Learning-assisted optimization for transmission switching
Abstract
The design of new strategies that exploit methods from machine learning to facilitate the resolution of challenging and large-scale mathematical optimization problems has recently become an avenue of prolific and promising research. In this paper, we propose a novel learning procedure to assist in the solution of a well-known computationally difficult optimization problem in power systems: The Direct Current Optimal Transmission Switching (DC-OTS) problem. The DC-OTS problem consists in finding the configuration of the power network that results in the cheapest dispatch of the power generating units. With the increasing variability in the operating conditions of power grids, the DC-OTS problem has lately sparked renewed interest, because operational strategies that include topological network changes have proved to be effective and efficient in helping maintain the balance between generation and demand. The DC-OTS problem includes a set of binaries that determine the on/off status of the switchable transmission lines. Therefore, it takes the form of a mixed-integer program, which is NP-hard in general. In this paper, we propose an approach to tackle the DC-OTS problem that leverages known solutions to past instances of the problem to speed up the mixed-integer optimization of a new unseen model. Although our approach does not offer optimality guarantees, a series of numerical experiments run on a real-life power system dataset show that it features a very high success rate in identifying the optimal grid topology (especially when compared to alternative competing heuristics), while rendering remarkable speed-up factors.
Keywords: Machine learning; Mathematical optimization; Mixed-integer programming; Optimal power flow; Optimal transmission switching.
© The Author(s) 2024.
Conflict of interest statement
Conflict of interestThe authors declare no Conflict of interest.
Figures



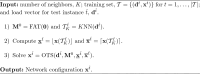




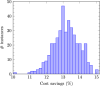


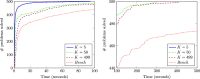
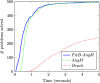
References
-
- Barrows C, Blumsack S, Bent R (2012) Computationally efficient optimal transmission switching: Solution space reduction. In: 2012 IEEE Power and Energy Society General Meeting, pp 1–8
-
- Bengio Y, Lodi A, Prouvost A (2021) Machine learning for combinatorial optimization: a methodological tour d’horizon. Eur J Oper Res 290(2):405–421. 10.1016/j.ejor.2020.07.063
-
- Blumsack S (2006) Network topologies and transmission investment under electric-industry restructuring. Carnegie Mellon University, Pittsburgh, Pennsylvania
-
- Bugaje A-AB, Cremer JL, Strbac G (2023) Real-time transmission switching with neural networks. IET Gener, Transm Distrib 17(3):696–705. 10.1049/gtd2.12698
-
- Cappart Q, Chételat D, Khalil EB, Lodi A, Morris C, Veličković P (2023) Combinatorial optimization and reasoning with graph neural networks. J Mach Learn Res 24(130):1–61
LinkOut - more resources
Full Text Sources
Miscellaneous
