Universal control of four singlet-triplet qubits

Abstract

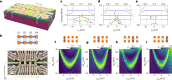
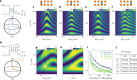
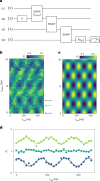
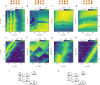
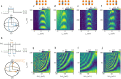
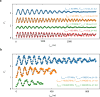
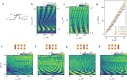
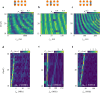
The coherent control of interacting spins in semiconductor quantum dots is of strong interest for quantum information processing and for studying quantum magnetism from the bottom up. Here we present a 2 × 4 germanium quantum dot array with full and controllable interactions between nearest-neighbour spins. As a demonstration of the level of control, we define four singlet-triplet qubits in this system and show two-axis single-qubit control of each qubit and SWAP-style two-qubit gates between all neighbouring qubit pairs, yielding average single-qubit gate fidelities of 99.49(8)-99.84(1)% and Bell state fidelities of 73(1)-90(1)%. Combining these operations, we experimentally implement a circuit designed to generate and distribute entanglement across the array. A remote Bell state with a fidelity of 75(2)% and concurrence of 22(4)% is achieved. These results highlight the potential of singlet-triplet qubits as a competing platform for quantum computing and indicate that scaling up the control of quantum dot spins in extended bilinear arrays can be feasible.

Fig. 1. Device and energy spectroscopy.

a, Schematic drawing showing the Ge/SiGe heterostructure and three layers of gate electrodes on top to define the quantum dot ladder and sensing dots: screening gates (purple), plunger gates (red) and barrier gates (green). Ohmic contacts (grey) extend towards the germanium quantum well in which the holes are confined. The aluminium oxide dielectric between different gate layers is omitted for clarity. b, False-coloured scanning electron microscope image of a device nominally identical to that used in the measurements. The eight quantum dots are labelled 1–8 and the four charge sensors to measure the charge states in the quantum dots are labelled S_TL, S_TR, S_BL and S_BR, respectively. The quantum dot potentials are controlled by plunger gates P_i, and the interdot or dot–sensor tunnel couplings are controlled by barrier gates b_ij or b_i, with i or j denoting the corresponding quantum dot number. A schematic of the ladder structure of the quantum dots is shown on top, with Q1–Q4 formed by vertical DQDs. c–e, The energy levels of two-spin states in a DQD as a function of energy detuning ε_ij between dot i and j with $J\left({\epsilon }_{ij}=0\right)<{\overline{E}}_z\left(\mathbf{c}\right),J\left({\epsilon }_{ij}=0\right)={\overline{E}}_z\left(\mathbf{d}\right),J\left({\epsilon }_{ij}=0\right)>{\overline{E}}_z\left(\mathbf{e}\right)$. The dashed black circles denote the positions of S–T₋ anticrossings. f–i, The measured energy spectra that probe the positions of the S–T₋ anticrossings as a function of the detuning (ε_ij) and the barrier gate voltage (vb_ij) for the vertical DQDs 1–5 (f), 2–6 (g), 3–7 (h) and 4–8 (i) at B = 5 mT. The colour scale shows the measured spin triplet probability P_T after initializing a vertical DQD in a singlet state (in (0,2) or (2,0)) and applying a gate voltage pulse (20 ns ramp in, 50 or 60 ns wait time, 0 ns ramp out to the PSB regime for readout) to the detuning shown on the horizontal axis, for different vb_ij. The 20 ns ramp-in time is used to ensure adiabaticity with respect to the tunnel coupling (2 GHz), while maintaining diabaticity relative to the S–T₋ anticrossing. The wait time is close to a π rotation to obtain a sizable triplet probability. The cartoons on top of the panels f–i represent the eight dots, and the dark grey line indicates which exchange coupling is active in the panel below.

Fig. 2. Universal single-qubit control of four singlet–triplet qubits.

a,b, The pulse schemes used for x-axis control (a) and y-axis control (b). In the experiments, the detuning pulse in a and b has a 20 ns ramp (not shown) from (2,0) to (1,1), similar to the pulse used for the energy spectroscopy. c–f, Experimental results for x-axis rotations of Q1 (c), Q2 (d), Q3 (e) and Q4 (f), showing measured triplet probabilities P_T as a function of t_wait and the corresponding barrier voltage δvb_ij. g, Measured P_T for the sequence shown in b as a function of t_wait and the barrier voltage change δvb₂₆. The position where $\sqrt{Y}$ is properly calibrated is indicated by a white dot. h, The numerically computed P_T as a function of t_wait and the ratio of the z-axis component to the x-axis component, $\left(J-{\overline{E}}_z\right)/{\mathrm{\Delta }}_{{\mathrm{ST}}_{-}}$. The parameters used for the calculation are extracted from g. i, Single-qubit RB data for Q1–Q4, with P_S the measured probabilities of the target state. The 95% confidence intervals based on statistical fluctuations are smaller than the data points. The numbers in the legend are the extracted average gate fidelities, which are obtained from the Clifford gate fidelities using a ratio of 3.625 (see Extended Data Table 1 for the detailed gate decomposition). The errors represent the 68% confidence intervals (Methods). j, Table showing the single-qubit gate fidelities of Q1–Q4 measured by GST. The errors represent the 95% confidence intervals computed using the Hessian of the log-likelihood function. All the data above are measured at B = 5 mT.

Fig. 3. Two-qubit interactions across the quantum dot ladder.

a, A representation of two connected DQDs. The S–T₋ qubits have a splitting of $J_{ij}-{\overline{E}}_{z,ij}$ and $J_{kl}-{\overline{E}}_{z,kl}$ (neglecting ${\mathrm{\Delta }}_{{\mathrm{ST}}_{-}}$), which are controlled by the detunings ε_ij and ε_kl, respectively. The qubit–qubit coupling J_coup is an average of J_ik and J_jl between the corresponding dots, which are controlled by ε_ik and ε_jl. b, The energy levels of two-qubit states, where we fix ε_kl to be positively large and scan ε_ij. At the positions where $J_{ij}-{\overline{E}}_{z,ij}$ equals $J_{kl}-{\overline{E}}_{z,kl}$, an anticrossing with a gap J_coup forms (black dashed circles), which can be used to induce SWAP oscillations between $∣{\mathrm{ST}}_{-}⟩$ and $∣{\mathrm{T}}_{-}\mathrm{S}⟩$. The parameters used in this calculation are based on the experimental results for Q3–Q4 shown in Supplementary Fig. 4c. c, The pulse scheme for SWAP operations. We start in (0,2) or (2,0), at large positive or negative detuning, and diabatically pulse one qubit to (1,1) at modest detuning such that it remains in $∣\mathrm{S}⟩$, and pulse the other qubit to zero detuning where a π rotation for a time t_X takes it to $∣{\mathrm{T}}_{-}⟩$ (other qubits are either initialized to singlets by pulsing back and forth to (0,2) or (2,0), or remain in the (1,1) regime all the time). At this point, the qubits are set to $∣{\mathrm{ST}}_{-}⟩$ or $∣{\mathrm{T}}_{-}\mathrm{S}⟩$. Next, we pulse the detunings of both qubits to make their energies resonant, while at the same time activating J_ik and J_jl. This will kickstart SWAP oscillations between the two qubits. The dashed lines in the pulse of ε_ij show that we scan the detuning of one qubit to find the condition for SWAP operations. After an evolution time t_wait, we pulse the detunings to the PSB readout configuration for one of the qubits. d–f, The experimental results of SWAP oscillations, showing measured singlet probabilities P_S as a function of operation time t_wait and the detuning voltage ε_ij for Q1–Q2 (d), Q2–Q3 (e) and Q3–Q4 (f). The initial states of two qubits (before the SWAP oscillations) are denoted on the top, and the qubit pair that is read out is indicated by the dashed arrow showing the readout pulse direction. g, The quantum circuit used to create a generalized Bell state between Q1 and Q2 and to characterize it via QST. h, Measured two-qubit density matrix of Q1–Q2, after removal of SPAM errors and using maximum-likelihood estimation (MLE). i, State fidelities and concurrence estimated from the density matrices of the Bell states of Q1–Q2, Q2–Q3 and Q3–Q4. The errors show the uncertainty with 68% confidence intervals (Methods). The data in panels d–f and h,i are measured at B = 5 mT (see Supplementary Note V for additional data taken at B = 10 mT).

Fig. 4. Implementation of a quantum circuit for entanglement generation and quantum state transfer.

a, Quantum circuit with all the qubits initialized into the singlet. An X gate (32 ns) rotates Q2 into a triplet state, and a SWAP interaction for a variable time t_SWAP periodically produces entanglement between Q1 and Q2. Two subsequent SWAP gates (30 ns and 24 ns) transfer the state of Q2 to Q4 and a final single-qubit rotation of Q4 for a variable time t_Q4 is followed by Q4 readout. The delay time between each quantum gate is set to zero. For more details, see Supplementary Note VI. b,c, Experimental (b) and numerical (c) results after running the quantum circuit shown in a, with triplet probabilities P_T of Q4 shown as a function of t_SWAP and t_Q4. The coloured arrows in b show the positions of the linecuts in d. d, Linecuts from a showing triplet probabilities P_T of Q4 as a function of control time t_Q4, with t_SWAP = 0, 4 and 7 ns (from bottom up). The data are vertically shifted by 0.5 for clarity. The 95% confidence intervals based on statistical fluctuations are smaller than the data points. All the data above are measured at B = 10 mT.

Extended Data Fig. 1. Charge stability diagrams and Pauli spin blockade.

a-d, Charge stability diagrams for DQD 1-5 (a), 2-6 (b), 3-7 (c), and 4-8 (d), respectively. a and b are recorded using the sensor S_BL while c and d are recorded using the sensor S_BR. Hole numbers inside the relevant charge stability regions are indicated, showing all the DQDs can be emptied to (0,0). e-h, Charge stability diagrams measured by scanning the detuning ε_ij and the overall chemical potential μ_ij of the DQD. The PSB regions inside the (2, 0) or (0, 2) area are indicated by solid white triangles and trapezoids. For outer DQD 1-5 and 4-8, we find PSB by pulsing ε₁₅ and ε₄₈ from (1,1) to (2,0) and (0,2), where within a triangular region an electron tunnels between the dots starting from the S(1, 1) but no tunnelling occurs from T₀(1, 1), T₋(1, 1) and T₊(1, 1) due to PSB. For inner DQD 2-6 and 3-7, we swap their spin states to those of DQD 5-6 and 7-8 where the sensor signals are stronger. i,j, Illustration of PSB using the energy levels in the quadruple quantum dot plaquette for DQD 2-6 (i) and 3-7 (j), respectively. The hole numbers are indicated as $\left(\begin{array}{cc}\hfill n_1,& \hfill n_2\hfill \\ \hfill n_5,& \hfill n_6\hfill \end{array}\right)$ for i and $\left(\begin{array}{cc}\hfill n_3,& \hfill n_4\hfill \\ \hfill n_7,& \hfill n_8\hfill \end{array}\right)$ for j, and the subscripts S and T show the two-spin states of holes in the quantum dots indicated by bold numbers, respectively. The solid arrows show fast spin-conserving tunnelling while the dashed arrows show suppressed tunnelling due to PSB. Here we take pair 2-6 as an example to explain the readout process of the inner spin pairs. First, we align DQD 1-5 at the charge stability boundary between (2,0) and (2,1), as shown by the white dot in e, and then pulse ε₂₆ from negative to positive. We subsequently find a shaded region between (0,1) and (0,2) in the diagram for DQD 2-6, which is caused by PSB in DQD 5-6. The mechanism is shown in i: when we pulse DQD 2-6 to the point where S(0, 2) is lower in energy than (0, 1), the holes in DQD 2-6 moves across to DQD 5-6, irrespective of the spin states. Subsequently, the conventional PSB mechanism in DQD 5-6 allows S(1, 1) to transition to S(0, 2), while the triplets T(1, 1) have to remain in the (1,1) charge state. In this way, we indirectly realize spin-to-charge conversion for the two spins initially in DQD 2-6. Actually, S(1, 1) in DQD 2-6 can also directly tunnel to S(0, 2) inside the same DQD, as seen by the curved arrow in i. The mechanism to measure DQD 3-7 is analogous.

Extended Data Fig. 2. Data of two-axis qubit control around the x- and z-axis, measured at B = 10 mT.

a,b, Pulse scheme and Bloch sphere illustration of x-axis and z-axis evolution of S − T₋ qubits. The straight blue and orange arrows show the corresponding rotation axis. The x-axis rotations are set by the S − T₋ coupling, ${\mathrm{\Delta }}_{S{T}_{-}}$. For large J such that $J-{\overline{E}}_z\gg {\mathrm{\Delta }}_{S{T}_{-}}$, the rotation axis tilts towards the z-axis. The rotation is never exactly around the z-axis due to the presence of a finite ${\mathrm{\Delta }}_{S{T}_{-}}$, yet, sufficiently orthogonal control is possible when $\left(J-{\overline{E}}_z\right)\gg {\mathrm{\Delta }}_{S{T}_{-}}$. In b, we illustrate a Ramsey-like pulse sequence used to demonstrate z-axis control. We first initialize the qubit into a singlet, perform a π/2 rotation around the x-axis of duration t_π/2, and then change J diabatically by pulsing the corresponding barrier gate by an amount δvb_ij to implement a z-axis rotation. Finally, we perform another π/2 operation around the x-axis and project the qubit into the S − T₋ basis for spin readout. c-f, Experimental results for x-axis rotations of each qubit, showing measured triplet probabilities P_T as a function of t_wait and the detuning voltage ε_ij. g-j, Experimental results for z-axis rotations of each qubit, showing P_T as a function of t_wait and the barrier voltage change δvb_ij. The oscillation frequency is given by $f_{S{T}_{-}}=\sqrt{{\left(J-{\overline{E}}_z\right)}^2+{\mathrm{\Delta }}_{S{T}_{-}}^2}/h$, where h is Planck’s constant. We note that the outer two barrier gates vb₁₅ and vb₄₈ have a stronger effect on the corresponding J_ij than the inner barrier gates vb₂₆ and vb₃₇. This may be explained by additional residual resist below the inner barrier gates, which are fabricated in the last step, and by the different fan-out routing for the outer barrier gates (see Fig. 1a,b in the main text). Within the tuning range of the barrier gate, the highest ratio $\left(J-{\overline{E}}_z\right)/{\mathrm{\Delta }}_{S{T}_{-}}$ amounts to around 20 for the outer qubits Q1 and Q4 and about 10 for the inner qubits Q2 and Q3 (see Supplementary Information IV for more details).

Extended Data Fig. 3. Decoherence times of the qubits under control.

a, Measured triplet probabilities P_T of long-time evolutions around the x-axis for Q1–Q4 at B=5 mT. b, Measured singlet probabilities P_S as a function of the evolution time t_wait at the centre of the chevron patterns of the SWAP oscillations for each pair of qubits at B=5 mT. The data of a and b are fitted with a function of the form $P_T=P_0+A\cos \left(2\pi ft+\varphi \right)\exp \left[-{\left(t/T^{*}\right)}^{\beta }\right]$, where P₀, A, β, f, T^* are fitting parameters. Here f refers to the oscillation frequency, T^* refers to $T_x^{*}$, the coherence time under x-axis rotations, or $T_{Qi-Qj}^{*}$, the coherence time under SWAP oscillations between adjacent qubits. Furthermore, the parameter β determines the shape of the decay envelope, and the fitted values are shown in the inset. β provides insight into the noise spectrum within the system: when quasi-static or low-frequency noise dominates, β = 2, leading to Gaussian decay; whereas when high-frequency noise prevails, β = 1, resulting in exponential decay. The extracted β for the x-axis rotations of Q1-Q3 and all the SWAP oscillations are close to 2, indicating the dominance of low-frequency noise in this system. Notice the large value of β for the x-axis rotations of Q4 may result from the fitting error. The errors represent the 68% confidence intervals obtained from fitting.

Extended Data Fig. 4. Coherent control of singlet-triplet states under different conditions and the average g-factor.

a, Pulse scheme to measure S − T₋ and S − T₀ oscillations. A square pulse is used with a ramp-in time t_ramp and waiting time t_wait. b, Measured triplet probabilities of DQD 4-8 as a function of t_wait and the barrier voltage amplitude δvb₄₈ with t_ramp = 20 ns. As mentioned in the main text, a block pulse along the detuning axis with 20-nanosecond ramp time (t_ramp) from (0,2) to (1,1) is adiabatic with respect to the tunnel coupling but diabatic with respect to the S − T₋ anticrossing. Therefore, we can drive x-rotations of S − T₋ qubits when the pulse amplitude reaches zero detuning with $J\left({\epsilon }_{ij}=0\right)~\overline{E_z}$ (see Fig. 1d in the main text). However, when we increase the barrier voltage change δvb₄₈ until $J\left({\epsilon }_{ij}=0\right)<\overline{E_z}$ (δvb₄₈ ~ 40 mV), the S − T₋ anticrossings appear away from zero detuning (see Fig. 1c in the main text), thus the same pulse does not produce x-axis oscillations of the S − T₋ qubit. Moreover, under this condition, the S − T₀ splitting is reduced and the 20-nanosecond ramp time eventually becomes diabatic with respect to the S − T₀ splitting. As a result, the singlet state will rotate between the S and T₀ states under the Zeeman energy difference between the two dots ΔE_z. c, Measured triplet probabilities of DQD 4-8 as a function of t_wait and t_ramp with δvb₄₈ = 40 mV. When t_ramp is small, the observed oscillations are between S and T₀; however, when t_ramp is increased until the pulse is adiabatic with respect to the S − T₀ splitting (over 100 ns), the S − T₀ oscillations can no longer be observed. Such a long ramp time can rotate the initial state to a superposition state between S and T₋ states, and z-axis rotations of the S − T₋ qubit become visible. Therefore, we also observe a transition of S − T₀ oscillations and S − T₋ oscillations as a function of t_ramp in the figure. d, The rotation frequency $f_{S{T}_{-}}$ of each qubit as a function of the magnetic field strength B. When the external magnetic field strength is varied while keeping the gate voltages fixed, the frequency of these S − T₋ oscillations increases nearly linearly with the field due to the contribution from Zeeman energy in $f_{S{T}_{-}}$. From the slope, we extract ${\overline{g}}_{ij}$ for the four qubits as shown in the inset. The errors represent the 68% confidence intervals obtained from fitting. The data are acquired using the fast Fourier transform (FFT) of time-domain oscillations in e-h. e-h, Measured singlet probabilities P_S of Q1 (i), Q2 (j), Q3 (k), and Q4 (l) as a function of t_wait and magnetic field strength B. The rotations are induced using the pulse scheme of panel a with t_ramp = 100 ns.

Extended Data Fig. 5. Coherent control of S − T₀ states and g-factor differences.

a-c, Measured singlet probabilities P_S as a function of t_wait and the magnetic field strength B for Q1 (c), Q2 (d), and Q4 (e) during S − T₀ oscillations. Here t_ramp is set to zero and the barrier gate voltage is set such that $J\left({\epsilon }_{ij}=0\right)<\overline{E_z}$ to suppress unwanted S − T₋ oscillations. d-f, The fast Fourier transforms of the data in a-c, with a signal that can be line-fitted using the g-factor difference Δg_ij (inset) of two dots. The errors represent the 68% confidence intervals obtained from fitting. For Q3, we didn’t find S − T₀ oscillations, which may be because the corresponding Δg is too low to detect.

Extended Data Fig. 6. Results of single-qubit gate set tomography.

a-h Single-qubit Pauli transfer matrices (PTM) of the $\sqrt{X}$ gate (a-d) and $\sqrt{Y}$ gate (e-h) for Q1–Q4 (from left to right) obtained from gate set tomography. i-l, Estimated state preparation and measurement (SPAM) error probabilities from GST results for Q1–Q4, using the same method as used in. We find that the SPAM errors of Q2 and Q3 are worse than those of Q1 and Q4. There are two reasons. Firstly, the indirect PSB mechanism is more sensitive to the readout point we chose and the idling point of the other qubit. In particular, the readout fidelity of the triplet is lower when triplet relaxation is faster at the readout point. Secondly, the slower tunnelling rate from (0,2) or (2,0) to (1,1) causes an initialization error in some cases. Also, the instability of the charge sensor can contribute to the readout error, which makes the readout visibility vary between different measurements.

Extended Data Fig. 7. Sequential readout and joint probabilities of two qubits under SWAP oscillations.

a,b, Sequentially measured probabilities P_SS, P_TS, P_ST and P_TT of Q2 and Q3 as a function of t_wait and the detuning of Q3, ε₃₇, after initializing Q2–Q3 into $∣T_{-}S⟩$ (a) and $∣SS⟩$ (b). The data is acquired at B = 5 mT. In a, the out-of-phase signals in P_TS and P_ST observed around ε₃₇ = 1.5 mV are the result of the SWAP oscillations between these two qubits. A similar signal to P_TS but with lower visibility is observed in P_SS, which can be explained by the higher triplet readout error for Q2 than for Q3. The sequential readout is achieved by pulsing the barrier gate δvb₂₆ to -60 mV, where we measure Q3 first for a duration of 20 μs and simultaneously keep Q2 in the centre of (1,1) with sufficiently large J, where the Hamiltonian eigenbasis corresponds to the qubit readout basis^,,. In the next step of the sequence, Q2 is measured. In panel b, we do not observe any apparent leakage to $∣TT⟩$ but only see signs of single-qubit rotations at low detunings. This is expected given that, in this regime, the states $∣TT⟩$ are far away in energy from the other states (see Fig. 3b in the main text).

Extended Data Fig. 8. Quantum gate circuit and results for quantum state tomography of the Bell states.

a,c,f,i, Quantum circuit used to prepare and characterize a Bell state for different qubit pairs. In a, we plot the details of the single-qubit basis changes after the generation of the Bell state, where we apply a fixed wait time before performing gates on Q2 to keep its phase consistent through all the experiments. In c, SWAP gates are used to transfer the state of Q2 to Q1 and that of Q3 to Q4. Next Q1 and Q4 are measured simultaneously using two sensors. In f, two consecutive SWAP gates are used to transfer Q3 to Q1. Next Q1 and Q4 are measured simultaneously using two sensors as well. In i, the quantum information is transferred from Q2 to Q4 before performing the single-qubit gates for basis changes. This allows us to quantify the entanglement between Q1 and Q4 after state transfer. d,g,j, Two-qubit density matrices obtained from the corresponding quantum circuit after removal of measurement errors and using MLE for Q2–Q3 (d), Q3–Q4 (g) and Q1–Q4 (j) (Fig. 3h shows the density matrix for Q1–Q2). Measurement errors were removed based on the SPAM matrices. These matrices include not only measurement errors but also initialization errors, hence we are overcorrecting. The fact that initialization errors for most qubits were much smaller than measurement errors combined with the fact that MLE forces the resulting density matrix to be physical, helps ensure a reliable outcome. If we don’t attempt to remove readout errors, the density matrices show state fidelities and concurrences of 71.3(6)% and 9(2)% for Q1–Q2, 64.2(6)% and 10(2)% for Q2–Q3, 64.6(7)% and 0(0)% for Q3–Q4 and 64.4(9)% and 0(0)% for Q1–Q4. The errors represent the 68% confidence intervals (Methods). b,e,h,k, SPAM matrices used in the quantum state tomography analysis of Q1–Q2 (b), Q2–Q3 (e), Q3–Q4 (h) and Q1–Q4 (k). The SPAM matrices of Q1–Q2 and Q1–Q4 were measured directly by initializing them to the indicated states and measuring the corresponding pair in a single-shot manner. For Q2–Q3 or Q3–Q4, we initialized the qubits to the indicated states and measured the state of Q1–Q4 after the SWAP operations. These SPAM matrices do include errors from the SWAP operations.

Extended Data Fig. 9. Measurement sequence and results of two-qubit gate set tomography.

a, Illustration of the gate voltage pulses for a two-qubit circuit. Performing a single-qubit gate in the two-qubit space is nontrivial since during the time one qubit is undergoing an operation, the idling qubit could suffer from unwanted rotations and crosstalk. To solve this problem, we pulse the idle qubit to an operating point where it completes a 2π rotation during the time needed to operate on the other qubit (see Supplementary Information VIII for more details). b-e, Measured PTMs obtained from GST for single-qubit gates in the two-qubit space, including ${\sqrt{X}}_{Q1}$ (b), ${\sqrt{X}}_{Q2}$ (c), ${\sqrt{Y}}_{Q1}$ (d) and ${\sqrt{Y}}_{Q2}$ (e). f-i, The ideal PTMs from GST for single-qubit gates in the two-qubit space, including ${\sqrt{X}}_{Q1}$ (f), ${\sqrt{X}}_{Q2}$ (g), ${\sqrt{Y}}_{Q1}$ (h) and ${\sqrt{Y}}_{Q2}$ (u). j, SPAM error matrix of the measured two qubits estimated from GST, using the same method as used in. k, The PTM of the standard $\sqrt{\mathrm{SWAP}}$ based on an isotropic Heisenberg exchange Hamiltonian. l, The experimentally measured PTM, $M_{\exp }$, obtained from GST. m, The theoretical PTM, M_the, of the $\sqrt{\mathrm{SWAP}}$-style gate obtained by fitting the experimentally measured PTM, $M_{\exp }$, with a PTM generated by Eq. (28) in Supplementary Information VII (the fitted parameters are given there). The Hamiltonian Eq. (28) includes effects of spin–orbit coupling that are left out in the Hamiltonian of Eq. (2) of the main text. The fidelity of the $\sqrt{\mathrm{SWAP}}$-style gate is obtained from $F=\frac{1}{d+1}\left(\mathrm{Tr}\left[M_{\mathrm{the}}^{-1}{M}_{\exp }\right]/d+1\right)$, where d = 2^N is the dimension of the Hilbert space, and N refers to the number of qubits.