Entropic Graph-based Posterior Regularization
- PMID: 39483441
- PMCID: PMC11526501
Entropic Graph-based Posterior Regularization
Abstract
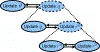
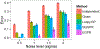
Graph smoothness objectives have achieved great success in semi-supervised learning but have not yet been applied extensively to unsupervised generative models. We define a new class of entropic graph-based posterior regularizers that augment a probabilistic model by encouraging pairs of nearby variables in a regularization graph to have similar posterior distributions. We present a three-way alternating optimization algorithm with closed-form updates for performing inference on this joint model and learning its parameters. This method admits updates linear in the degree of the regularization graph, exhibits monotone convergence, and is easily parallelizable. We are motivated by applications in computational biology in which temporal models such as hidden Markov models are used to learn a human-interpretable representation of genomic data. On a synthetic problem, we show that our method outperforms existing methods for graph-based regularization and a comparable strategy for incorporating long-range interactions using existing methods for approximate inference. Using genome-scale functional genomics data, we integrate genome 3D interaction data into existing models for genome annotation and demonstrate significant improvements in predicting genomic activity.
Figures

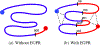

References
-
- Altun Yasemin, Belkin Mikhail, and Mcallester David A. Maximum margin semi-supervised learning for structured variables. In NIPS, pp. 33–40, 2005.
-
- Bishop C Neural Networks for Pattern Recognition. Oxford UP, Oxford, UK, 1995.
-
- Chapelle O, Zien A, and Schölkopf B (eds.). Semi-supervised learning. MIT Press, 2006.
Grants and funding
LinkOut - more resources
Full Text Sources
