A scenario for an evolutionary selection of ageing

Abstract

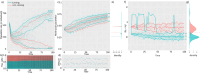
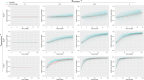
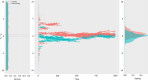
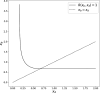
Signs of ageing become apparent only late in life, after organismal development is finalized. Ageing, most notably, decreases an individual's fitness. As such, it is most commonly perceived as a non-adaptive force of evolution and considered a by-product of natural selection. Building upon the evolutionarily conserved age-related Smurf phenotype, we propose a simple mathematical life-history trait model in which an organism is characterized by two core abilities: reproduction and homeostasis. Through the simulation of this model, we observe (1) the convergence of fertility's end with the onset of senescence, (2) the relative success of ageing populations, as compared to non-ageing populations, and (3) the enhanced evolvability (i.e. the generation of genetic variability) of ageing populations. In addition, we formally demonstrate the mathematical convergence observed in (1). We thus theorize that mechanisms that link the timing of fertility and ageing have been selected and fixed over evolutionary history, which, in turn, explains why ageing populations are more evolvable and therefore more successful. Broadly speaking, our work suggests that ageing is an adaptive force of evolution.

Keywords: adaptability; ageing evolution; differential inclusion; evolutionary biology; none; two phases model.

Figure 1.. Three typical configurations of the model with i_b >i_d and their effect on progeny’s genotypes as a function of parental age.

(upper panel) Each haploid individual is defined by a parameter x_b defining its fertility span of intensity i_b and a parameter x_d defining the time during which it will maintain itself, with an intensity i_d. These parameters can be positive or null. (a) ’Too young to die’: it corresponds to configurations satisfying x_d <x_b. (b) ’Now useless’: it corresponds to configurations where x_b = x_d. (c) ‘Menopause’: it corresponds to configurations where x_d >x_b. (lower panel) Each individual may randomly produce a progeny during its fertility span [0; x_b]. (d) In the case of physiologically young parents (a<x_d), the progeny’s genotype is that of its parent ∓ a Gaussian kernel of mutation centered on the parental gene. In the case of the reproduction event occurring after x_d, for configuration (a) above, two cases are observed, (e) if the organism carries a Lansing effect ability, the x_d of its progeny will be strongly decreased. (f) In the absence of the Lansing effect, the default rule applies.

Figure 2.. The bd model shows a convergence of x_b - x_d towards a positive value.

Dynamics of the individual-based model shows a convergence of x_b - x_d towards a positive constant value in the absence of the Lansing effect. (a) The generalized b-d model shows a convergence of (x_b - x_d) for any i_b and i_d towards a positive value given by (b) (Annexe 4.3, Figure 2). (c) Simulation of 1000 individuals with initial trait (x_b=1.2, x_d=1.6) of intensities i_b=i_d=1, a competition c=0.0009 and a mutation kernel (P=0.1, σ=0.05) show that the two parameters co-evolvetowards x_b - x_d ≅ 0.55 that is log(3)/2. (d) Landscape of solutions (x_b - x_d) as a function of i_b and i_d (colors separate ranges of 50 units on the z-axis).

Figure 3.. The Lansing effect maximizes populational survival by increasing its evolvability.

100 independent simulations were run with a competition intensity of 9.10^–4 and a mutation rate p=0.1 on a mixed population made of 500 non-Lansing individuals and 500 individuals subjected to such effect. At t₀, the population size exceeds the maximum load of the medium thus leading to a population decline at start. At t₀, all individuals are of age 0. Here, we plotted a subset of the 100.10⁶ plus individuals generated during the simulations. Each individual is represented by a segment between its time of birth and its time of death. In each graph, blue and red curves represent deciles 1, 5, and 9 of the distribution at any time for each population type. (a) The higher success rate of Lansing bearing populations does not seem to be associated with a significantly faster population growth but with a lower risk of collapse. (b) For cohabitating populations, the Lansing bearing population (blue) is overgrowing by only 10% the non-Lansing one (red). (c) This higher success rate is associated with a faster and broader exploration of the Malthusian parameter - surrogate for fitness - space in Lansing bearing populations (d) that is not associated with significant changes in the lifespan distribution (e) but a faster increase in genotypic variability within the [0; 10] time interval. (f) This occurs although progeny from physiologically old parents can represent up to 10% of the Lansing bearing population and leads to it reaching the theoretical optimum within the timeframe of simulation (g) with the exception of Lansing progenies. (e–g) Horizontal lines represent the theoretical limits for (x_b - x_d) in Lansing (blue) and non-Lansing (red) populations.

Figure 3—figure supplement 1.. Evolution of the average Malthusian parameter value in Lansing and non-Lansing populations as a function of time.

p is the mutation rate and c is the logistic competition intensity. Individual values are plotted, the line represents the average value amongst populations. In all conditions with p > 0, the Malthusian parameter grows faster and remains slightly higher in the Lansing populations than in the non-Lansing ones.

Figure 3—figure supplement 2.. Evolution of the Lansing and non-Lansing populations size as a function of time.

p is the mutation rate and c is the logistic competition intensity.

Figure 4.. Mixed populations lead to (x_b - x_d) theoretical limit in a limited time and cohabitation of Lansing and non-Lansing populations.

Starting with a homogenous population of 5000 Lansing bearing and 5000 non-Lansing individuals with traits uniformly distributed from –10 to +10 (left panel), we ran 100 independent simulations on time in [0; 1000]. (center panel) Plotting the trait (x_b - x_d) as a function of time for one simulation shows a rapid elimination of extreme traits and branching evolution. (right panel) The final distribution of traits in each population type is centered on the theoretical convergence limit for each. N_total ≅ 110 millionindividuals, c=9.10^–4, p=0.1.

Figure 5.. The Lansing effect is associated with an increased fitness gradient.

We were able to derive Lansing and non-Lansing Malthusian parameters from the model’s equations (see Annexe 1–2.3 and 1–5) and plot them as a function of the trait (x_b, x_d). The diagonal x_b = x_d is drawn in light green. The corresponding isoclines are overlapping above the diagonal but significantly differ below, with non-Lansing fitness (red lines) being higher than that of Lansing’s (light blue lines). In addition, the distance between two consecutive isoclines is significantly more important in the lower part of the graph for non-Lansing than Lansing bearing populations. As such, a mutation leading a non-Lansing individual’s fitness going from 0.7 to 0.8 (yellow arrow) corresponds to a Lansing individual’s fitness going from 0.1 to 0.52. Finally, Hamilton’s decreasing force of selection with age can be observed along the diagonal with a growing distance between two consecutive fitness isoclines as x_b and x_d continue increasing.

Appendix 1—figure 1.. The set V={(xb,xd)∈R+2;R(xb,xd)>1} is the convex set delimited by the black curve with equation R(xb,xd)=1.

Appendix 1—figure 2.. Simulation of the canonical equation with x0=(3.5,1.3) and ib=id=1.

(a) Dynamics of x_b. (b) Dynamics of x_d. (c) Dynamics of, ${\displaystyle x_b-x_d}$ the black curve has equation. ${\displaystyle y=\log (3)/2}$.

Appendix 1—figure 3.. Optimal configurations as time tends to infinity.