Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2024 Oct 10;10(20):e39136.
doi: 10.1016/j.heliyon.2024.e39136. eCollection 2024 Oct 30.

Conjunctive optimal operation of water and power networks

Tomer Shmaya  1 , Mashor Housh  2 , Filippo Pecci  3 , Kyri Baker  4 , Joseph Kasprzyk  4 , Avi Ostfeld  5
Affiliations

Conjunctive optimal operation of water and power networks

Tomer Shmaya et al. Heliyon. .

Abstract

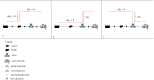
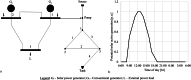
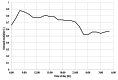
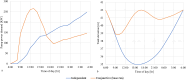
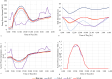
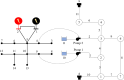
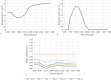
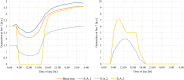
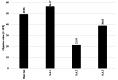
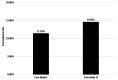
Water distribution systems (WDSs) are designed to convey water from sources to consumers. Their operation is a main concern for engineers, researchers, and practitioners and is subject to demand, pressure, and quality constraints. Pumping stations require power to pump water and keep system pressure at a desired level. On the other hand, power is generally supplied through power grids (PGs), which require optimal operation while satisfying operational constraints, such as generation limits, power consumption, and voltage constraints. Since the two infrastructure systems are interconnected, decision-makers could benefit from a holistic approach that would allow solving the two operational optimization problems together as one conjunctive problem. This paper presents the full mathematical formulation of the conjunctive optimization problem, including a novel modelling approach for the operation of a variable speed pump, which does not include integer variables for pump status, thus allowing to solve the model as a non-linear programming (NLP) problem. The formulation is applied to two illustrative case studies, and the results are compared to the optimal operation of the independent WDS. The inclusion of the PG in the optimization problem is observed clearly in the results and influences them quite significantly. WDS operation is shown adjust to the PG constraints, and the application of the conjunctive model results in a cost reduction rate of more than 10 % for both case studies.

Keywords: Optimal operation; Optimal power flow; Water distribution systems; Water-energy nexus.

PubMed Disclaimer

Conflict of interest statement

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Figures

Fig. 1
Fig. 1
Modelling of variable speed pumps.
Fig. 2
Fig. 2
Case study I – system layout and solar profile.
Fig. 3
Fig. 3
Water demand pattern.
Fig. 4
Fig. 4
Case study I – base run results.
Fig. 5
Fig. 5
Case study I – base run results - pump status chart.
Fig. 6
Fig. 6
Case study I – sensitivity analysis results – WDS response.
Fig. 7
Fig. 7
Case study I – sensitivity analysis results – power grid response.
Fig. 8
Fig. 8
Case study I – sensitivity analysis objectives.
Fig. 9
Fig. 9
Case study II – system layout.
Fig. 10
Fig. 10
Case study II – base run results - WDS.
Fig. 11
Fig. 11
Case study II – base run results – pump status chart.
Fig. 12
Fig. 12
Case study II – base run results - power grid.
Fig. 13
Fig. 13
Case study II - sensitivity analysis results – WDS response.
Fig. 14
Fig. 14
Case study II – sensitivity analysis results – power grid response.
Fig. 15
Fig. 15
Case study I – sensitivity analysis objectives.
Fig. 16
Fig. 16
Cost reduction rates.
See this image and copyright information in PMC

References

    1. Dai J., Wu S., Han G., Weinberg J., Xie X., Wu X., Song X., Jia B., Xue W., Yang Q. Water-energy nexus: a review of methods and tools for macro-assessment. Appl. Energy. 2018;210:393–408. doi: 10.1016/j.apenergy.2017.08.243. - DOI
    1. Giustolisi O., Laucelli D.B., Berardi L. Operational optimization: water losses versus energy costs. J. Hydraul. Eng. 2013;139(4):410–423. doi: 10.1061/(asce)hy.1943-7900.0000681. - DOI
    1. Fooladivanda D., Taylor J.A. Energy-Optimal pump scheduling and water flow. IEEE Transactions on Control of Network Systems. 2018;5(3):1016–1026. doi: 10.1109/tcns.2017.2670501. - DOI
    1. Jowitt P., Germanopoulos G. Optimal pump scheduling in Water‐Supply networks. J. Water Resour. Plann. Manag. 1992;118(4):406–422. doi: 10.1061/(asce)0733-9496(1992)118:4(406. - DOI
    1. Stokes C., Simpson A.R., Maier H.R. A computational software tool for the minimization of costs and greenhouse gas emissions associated with water distribution systems. Environ. Model. Software. 2015;69:452–467. doi: 10.1016/j.envsoft.2014.11.004. - DOI

LinkOut - more resources