Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2024 Nov 8;14(1):27185.
doi: 10.1038/s41598-024-78140-9.

Transmission dynamics of fractional order SVEIR model for African swine fever virus with optimal control analysis

S Suganya  1 , V Parthiban  2 , L Shangerganesh #  3 , S Hariharan #  3   4
Affiliations

Transmission dynamics of fractional order SVEIR model for African swine fever virus with optimal control analysis

S Suganya et al. Sci Rep. .

Abstract

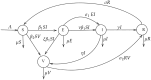
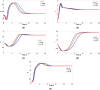
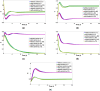
Understanding the dynamics of the African swine fever virus during periods of intense replication is critical for effective combatting of the rapid spread. In our research, we have developed a fractional-order SVEIR model using the Caputo derivatives to investigate this behaviour. We have established the existence and uniqueness of the solution through fixed point theory and determined the basic reproduction number using the next-generation matrix method. Our study also involves an examination of the local and global stability of disease-free equilibrium points. Additionally, we have conducted optimal control analysis with two control variables to increase the number of recovered pigs while reducing the number of those infected and exposed. We have supported our findings with numerical simulations to demonstrate the effectiveness of the control strategy.

Keywords: African swine fever; Caputo fractional derivative; Numerical Simulation.; Optimal control; Stability analysis.

PubMed Disclaimer

Conflict of interest statement

The authors have no competing interests to declare that are relevant to the content of this article.

Figures

Fig. 1
Fig. 1
Schematic process of the proposed work.
Fig. 2
Fig. 2
Schematic flowchart for SVEIR model.
Fig. 3
Fig. 3
Visualizes the dynamical behaviour of all pigs population with respect to days for a integer and non-integer values of formula image.
Fig. 4
Fig. 4
Graphical representation for S, V, E, I and R compartments with and without optimal controls for a integer and non-integer values of formula image.
Fig. 5
Fig. 5
Optimal control trajectory of formula image with integer and non-integer values of formula image.
See this image and copyright information in PMC

References

    1. Kouidere, A., Balatif, O. & Rachik, M. Analysis and optimal control of a mathematical modeling of the spread of African swine fever virus with a case study of South Korea and cost-effectiveness. Chaos, Solitons Fractals146, 110867 (2021).
    1. Mahroug, F. & Bentout, S. Dynamics of a diffusion dispersal viral epidemic model with age infection in a spatially heterogeneous environment with general nonlinear function. Math. Methods Appl. Sci.46, 14983–15010 (2023).
    1. Djilali, S., Bentout, S. & Tridane, A. Dynamics of a generalized nonlocal dispersion SIS epidemic model. J. Evol. Equ.24, 1–24 (2024). - PubMed
    1. Soufiane, B. & Touaoula, T. M. Global analysis of an infection age model with a class of nonlinear incidence rates. J. Math. Anal. Appl.434, 1211–1239 (2016).
    1. Djilali, S., Bentout, S., Kumar, S. & Touaoula, T. M. Approximating the asymptomatic infectious cases of the COVID-19 disease in Algeria and India using a mathematical model. Int. J. Model. Simul. Sci. Comput.13, 2250028 (2022).

LinkOut - more resources