Vector-borne disease outbreak control via instant releases

Abstract

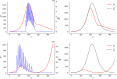
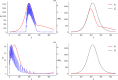
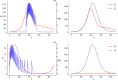
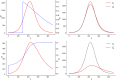
This paper is devoted to the study of optimal release strategies to control vector-borne diseases, such as dengue, Zika, chikungunya and malaria. Two techniques are considered: the sterile insect one (SIT), which consists in releasing sterilized males among wild vectors in order to perturb their reproduction, and the Wolbachia one (presently used mainly for mosquitoes), which consists in releasing vectors, that are infected with a bacterium limiting their vectorial capacity, in order to replace the wild population by one with reduced vectorial capacity. In each case, the time dynamics of the vector population is modeled by a system of ordinary differential equations in which the releases are represented by linear combinations of Dirac measures with positive coefficients determining their intensity. We introduce optimal control problems that we solve numerically using ad-hoc algorithms, based on writing first-order optimality conditions characterizing the best combination of Dirac measures. We then discuss the results obtained, focusing in particular on the complexity and efficiency of optimal controls and comparing the strategies obtained. Mathematical modeling can help testing a great number of scenarios that are potentially interesting in future interventions (even those that are orthogonal to the present strategies) but that would be hard, costly or even impossible to test in the field in present conditions.

Keywords: Dengue; Impulsive control; Optimal epidemic vector control; Sterile insect technique; Vector-borne diseases; Wolbachia.

Fig. 1

Results of the simulations for the SIT with $C=3\times {10}^7$ (upper row) and $C=6\times {10}^7$ (lower row) considering 10 releases. The dashed blue line corresponds to the amount of sterile mosquitoes present at each time and the its jumps correspond to the releases. $I_H^{\ast }$, on the right column, corresponds to the uncontrolled case (color figure online)

Fig. 2

Results of the simulations for the SIT with $C=3\times {10}^7$ (upper row) and $C=6\times {10}^7$ (lower row) considering 20 releases

Fig. 3

Results of the simulations for the SIT with $C=3\times {10}^7$ (upper row) and $C=6\times {10}^7$ (lower row) considering 10 releases and an equal distribution of the mosquitoes between the releases

Fig. 4

Results of the simulations for the SIT with $C=3\times {10}^7$ (upper row) and $C=6\times {10}^7$ (lower row) considering 20 releases and an equal distribution of the mosquitoes between the releases

Fig. 5

Results of the simulations for the Wolbachia method with $C=10000$ (upper row) and $C=20000$ (lower row). The proportion of Wolbachia infected mosquitoes corresponds to the dashed blue line on the left column. $I_H^{\ast }$, on the right column, corresponds to the uncontrolled case

Fig. 6

Evolution of the functional J(u) and $\sum c_i-C$ during the sterile insect simulation for 20 releases and $C=3\times {10}^7$