Tuning the BCS-BEC crossover of electron-hole pairing with pressure

Abstract

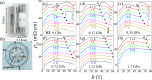
In graphite, a moderate magnetic field confines electrons and holes into their lowest Landau levels. In the extreme quantum limit, two insulating states with a dome-like field dependence of the their critical temperatures are induced by the magnetic field. Here, we study the evolution of the first dome (below 60 T) under hydrostatic pressure up to 1.7 GPa. With increasing pressure, the field-temperature phase boundary shifts towards higher magnetic fields, yet the maximum critical temperature remains unchanged. According to our fermiology data, pressure amplifies the density and the in-plane effective cyclotron mass of hole-like and electron-like carriers. Thanks to this information, we verify the persistent relevance of the BCS relation between the critical temperature and the density of states in the weak-coupling boundary of the dome. In contrast, the strong-coupling summit of the dome does not show any detectable change with pressure. We argue that this is because the out-of-plane BCS coherence length approaches the interplane distance that shows little change with pressure. Thus, the BCS-BEC crossover is tunable by magnetic field and pressure, but with a locked summit.

Fig. 1. Comparing a theoretical and an experimental phase diagram.

a The theoretical phase diagram for an excitonic insulator showing the evolution of the ordering energy as a function of the band gap^,. The order parameter is strongest when the band gap is zero. Note the contrast between the evolution of the order parameter on the two sides of the dome. b The experimental phase diagram of graphite at high magnetic field^,. The insulating state resides inside a dome in the (field, temperature) plane. A second dome (starting at  ≈3 T and ending at  ≈70 T) is not shown. Note the contrast between the gradual rise of the critical temperature to the summit of the dome and its abrupt drop afterwards.

Fig. 2. Pressure cell and magneto resistivity results.

a Photo of the pressure cell of external diameter 11.8 mm used in the pulsed-magnet. b Photo of a Kish graphite sample in the pressure cell. The pressure was determined in situ by the superconducting temperature transition of tin. c–h Field dependence of ρ_xx up to 60 T at various temperatures and for different pressures. Curves are shifted for clarity. The onset transition (α) and the re-entrant transition (${\alpha }^{\prime }$) of the first dome are indicated with black solid squares and red empty circles. The Shubnikov-de Haas oscillations at low-field are also observed at low temperatures (see Supplementary Note 2). The α and ${\alpha }^{\prime }$ are shifting to higher field after applied pressure. Under 1.12 Gpa, the ${\alpha }^{\prime }$ shifts beyond 60 T. Note c is the data without gasket and d–h are the ones with gasket.

Fig. 3. phase diagram of graphite under pressure.

a–f T − B phase diagrams for H∥c axis at the pressure of 0, 0.12, 0.35, 0.72, 1.12, and 1.7 GPa. The dome is shifting to higher field under hydrostatic pressure. In contrast, the summit of the dome is independent of the pressure. The two solid circles in the b show the kinks in magnetoresistance. h–m Tvs1/B at different pressure. The solid lines are a fit of the low-field boundary of phase α using Eq. (1), see the text. g, n Pressure dependence of the parameters T^* and B^* deduced from the fits.

Fig. 4. Pressure dependence of the Fermi surface properties of graphite.

a Pressure dependence of the SdH frequencies (F) of the electrons (blue) and holes (red). Insert: sketch of the Fermi surface of graphite, formed by six adjacent ellipsoid pockets (electron in blue and hole in red). b Pressure dependence of the in-plane effective cyclotron mass m* of the electrons (blue) and holes (red). c Pressure dependence of the Fermi energy of the electrons (blue) and holes (red). d Sketch of the Landau-level spectrum of graphite close to the summit of the dome. The solid curves represent the conditions at ambient pressure, while the dashed curves correspond to those under pressure. On the right, the corresponding density of states is depicted.

Fig. 5. BCS-BEC crossover in graphite.

a Field dependence of ξ_∥ (black open circle points, see the text for the definition), at ambient pressure compare with the field dependence of the critical temperature (T) in red square points. The purple dashed line is the A–A interlayer distance c₀. When ξ_∥ saturates to c₀, T saturates also at its largest value. The inset shows the lattice structure of graphite. b Field dependence of ξ_∥k_F,∥ at ambient pressure compare with the inter-pair coherence length ξk_F (blue full line) at the mean-field level vs. the coupling parameter ${\left(k_F{a}_F\right)}^{-1}$. Reproduced from ref. .